题目内容
若α为第二象限的角，则下列各式恒小于零的是（ ）
| A、sinα+cosα |
| B、tanα+sinα |
| C、sinα-cosα |
| D、sinα-tanα |
考点：三角函数值的符号
专题：三角函数的求值
分析：由α为第二象限的角，得到-1＜cosα＜0，从而得到1+
＜0，则答案可求．
| 1 |
| cosα |
解答：
解：∵α是第二象限的角，
∴-1＜cosα＜0，
∴tanα+sinα=sinα（1+
）＜0．
故选：B．
∴-1＜cosα＜0，
∴tanα+sinα=sinα（1+
| 1 |
| cosα |
故选：B．
点评：本题考查了三角函数的符号，考查了同角三角函数的基本关系式，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
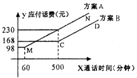电信局为满足不同客户的需要，设有A、B两种优惠方案，这两种方案应付话费（元）与通话时间（分钟）之间的关系如图（MN∥CD），若通话时间为500分钟，则应选择哪种方案更优惠（ ）| A、方案A | B、方案B |
| C、两种方案一样优惠 | D、不能确定 |
若数列{an}为等差数列，ap=q，aq=p（p≠q），则ap+q=（ ）
| A、p+q | ||
| B、0 | ||
| C、-（p+q） | ||
D、
|