题目内容
设函数f(x)=
.
(1)当a=-5时,求函数f(x)的定义域;
(2)若函数f(x)的定义域为R,试求a的取值范围.
| |x+1|+|x-2|+a |
(1)当a=-5时,求函数f(x)的定义域;
(2)若函数f(x)的定义域为R,试求a的取值范围.
考点:函数的定义域及其求法
专题:函数的性质及应用,不等式的解法及应用
分析:(1)由|x+1|+|x-2|-5≥0,然后构造函数y=|x+1|+|x-2|,在同一坐标系内画出函数y=|x+1|+|x-2|与y=5的图象得答案;
(2)函数f(x)的定义域为R,说明当x∈R时,恒有|x+1|+|x-2|+a≥0,即|x+1|+|x-2|≥-a,然后结合绝对值的几何意义求得a的取值范围.
(2)函数f(x)的定义域为R,说明当x∈R时,恒有|x+1|+|x-2|+a≥0,即|x+1|+|x-2|≥-a,然后结合绝对值的几何意义求得a的取值范围.
解答:
解:(1)由题设知:|x+1|+|x-2|-5≥0,
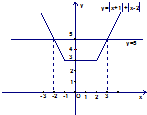
如图,在同一坐标系中作出函数y=|x+1|+|x-2|
和y=5的图象(如图所示),知定义域为(-∞,-2]∪[3,+∞);
(2)由题设知,当x∈R时,恒有|x+1|+|x-2|+a≥0,
即|x+1|+|x-2|≥-a,由(1)|x+1|+|x-2|≥3,
∴-a≤3,即a≥-3.
如图,在同一坐标系中作出函数y=|x+1|+|x-2|
和y=5的图象(如图所示),知定义域为(-∞,-2]∪[3,+∞);

(2)由题设知,当x∈R时,恒有|x+1|+|x-2|+a≥0,
即|x+1|+|x-2|≥-a,由(1)|x+1|+|x-2|≥3,
∴-a≤3,即a≥-3.
点评:本题考查了函数的定义域及其求法,考查了数形结合的解题思想方法,考查了绝对值的几何意义,是中档题.

练习册系列答案
相关题目
在下列四个函数中,满足性质:“对于区间(1,2)上的任意x1,x2(x1≠x2),|f(x2)-f(x1)|<|x2-x1|恒成立”的只有( )
A、f(x)=
| ||
| B、f(x)=|x| | ||
| C、f(x)=2 | ||
| D、f(x)=x2 |
若α为第二象限的角,则下列各式恒小于零的是( )
| A、sinα+cosα |
| B、tanα+sinα |
| C、sinα-cosα |
| D、sinα-tanα |
已知f(x)=(2-a)(x-1)-2lnx,g(x)=xe1-x.且f(x)>f'(x)对于x∈R恒成立(e为自然对数的底),则( )
| A、e2013•f(2014)>e2014•f(2013) |
| B、e2013•f(2014)=e2014•f(2013) |
| C、e2013•f(2014)<e2014•f(2013) |
| D、e2013•f(2014)与e2014•f(2013)大小不确定 |