题目内容
在△ABC中，已知2
•
=
|
|•|
|=3
2，则∠C= ．
| AB |
| AC |
| 3 |
| AB |
| AC |
| BC |
考点：平面向量数量积的运算
专题：计算题,解三角形,平面向量及应用
分析：运用数量积的定义，可得A，再由余弦定理，可得a，b，c的关系，根据三角形内角和定理，即可得到角C．
解答：
解：由于2
•
=
|
|•|
|=3
2，
则2|
|•|
|•cosA=
|
|•|
|，即有cosA=
，
由于A为三角形的内角，则A=
，
又设三角形的三个内角A，B，C所对的边为a，b，c，
则
cb=3a2，又由余弦定理，a2=b2+c2-2bccosA
=b2+c2-bc，即有
b2+
c2-4bc=0，
解得，b=
c或b=
c，
若b=
c，则a=c，即有C=A=
；
若b=
c，则a=
c，即有A=B=
，则C=π-
×2=
．
故答案为：
或
．
| AB |
| AC |
| 3 |
| AB |
| AC |
| BC |
则2|
| AB |
| AC |
| 3 |
| AB |
| AC |
| ||
| 2 |
由于A为三角形的内角，则A=
| π |
| 6 |
又设三角形的三个内角A，B，C所对的边为a，b，c，
则
| 3 |
=b2+c2-bc，即有
| 3 |
| 3 |
解得，b=
| 3 |
| ||
| 3 |
若b=
| 3 |
| π |
| 6 |
若b=
| ||
| 3 |
| ||
| 3 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
故答案为：
| π |
| 6 |
| 2π |
| 3 |
点评：本题考查平面向量的数量积的定义和性质，考查余弦定理的运用，考查运算能力，属于中档题．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
双曲线16x2-9y2=144的离心率e=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=ax2+bx+c与y=ax+b（ab≠0）的图象可能是（ ）
A、 |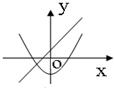
B、 |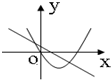
C、 |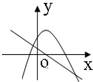
D、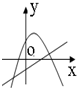 |