题目内容
设函数f(x)=alnx+
(a≠0)的图象上在点(1,f(1))处的切线l的斜率为2-3a,
(Ⅰ)求实数a的值;
(Ⅱ)求证:对于定义域内的任意一个x,都有f(x)≥3-x.
| 2a2 |
| x |
(Ⅰ)求实数a的值;
(Ⅱ)求证:对于定义域内的任意一个x,都有f(x)≥3-x.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:计算题,导数的综合应用
分析:(Ⅰ)求f(x)的定义域为{x|x>0},再求导f′(x)=
-
,从而可得a的值;
(Ⅱ)设g(x)=f(x)-(3-x),求导,化恒成立问题为最值问题.
| a |
| x |
| 2a2 |
| x2 |
(Ⅱ)设g(x)=f(x)-(3-x),求导,化恒成立问题为最值问题.
解答:
解:(Ⅰ)f(x)的定义域为{x|x>0},f′(x)=
-
.
根据题意,f'(1)=2-3a,所以a-2a2=2-3a,
即a2-2a+1=0,解得a=1.
(Ⅱ)证明:f(x)=lnx+
.
设g(x)=f(x)-(3-x),
即g(x)=lnx+
+x-3.g′(x)=
-
+1=
=
(x>0).
当x变化时,g'(x),g(x)的变化情况如下表:
x=1是g(x)在(0,+∞)上的唯一极值点,且是极小值点,从而也是g(x)的最小值点.
可见g(x)最小值=g(1)=0,
所以g(x)≥0,即f(x)-(3-x)≥0,
所以对于定义域内的每一个x,都有f(x)≥3-x.
| a |
| x |
| 2a2 |
| x2 |
根据题意,f'(1)=2-3a,所以a-2a2=2-3a,
即a2-2a+1=0,解得a=1.
(Ⅱ)证明:f(x)=lnx+
| 2 |
| x |
设g(x)=f(x)-(3-x),
即g(x)=lnx+
| 2 |
| x |
| 1 |
| x |
| 2 |
| x2 |
| x2+x-2 |
| x2 |
| (x-1)(x+2) |
| x2 |
当x变化时,g'(x),g(x)的变化情况如下表:
| x | (0,1) | 1 | (1,+∞) |
| g'(x) | - | 0 | + |
| g(x) | ↘ | 极小值 | ↗ |
可见g(x)最小值=g(1)=0,
所以g(x)≥0,即f(x)-(3-x)≥0,
所以对于定义域内的每一个x,都有f(x)≥3-x.
点评:本题考查了导数的综合应用,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
双曲线16x2-9y2=144的离心率e=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=ax2+bx+c与y=ax+b(ab≠0)的图象可能是( )
A、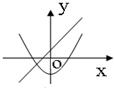 |
B、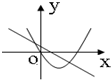 |
C、 |
D、 |