题目内容
设向量
=(a1,a2),
=(b1,b2),定义一种向量积
?
=(a1b1,a2b2),已知
=(2,
),
=(
,0),点P(x,y)在y=sinx的图象上运动.Q是函数y=f(x)图象上的点,且满足
=
?
+
(其中O为坐标原点),则当x∈[-
,
]时,函数y=f(x)的值域是 .
| a |
| b |
| a |
| b |
| m |
| 1 |
| 2 |
| n |
| π |
| 3 |
| OQ |
| m |
| OP |
| n |
| π |
| 6 |
| 2π |
| 3 |
考点:平面向量数量积的运算
专题:新定义,三角函数的图像与性质,平面向量及应用
分析:设P(x0,y0),则y0=sinx0,运用新定义,求得Q的轨迹方程,再由x的范围,求得
x-
的范围,再由正弦函数的单调性,即可得到值域.
| 1 |
| 2 |
| π |
| 6 |
解答:
解:设P(x0,y0),则y0=sinx0,
由新定义,可得,
=
?
+
=(2x0,
y0)+(
,0)
=(2x0+
,
y0),
即有x=2x0+
,且y=
y0,
即有x0=
x-
,y0=2y,
则有y=
sin(
x-
),
由于x∈[-
,
],则有
x-
∈[-
,
].
则有sin(
x-
)∈[-
,
],
则f(x)∈[-
,
].
故答案为:[-
,
].
由新定义,可得,
| OQ |
| m |
| OP |
| n |
| 1 |
| 2 |
| π |
| 3 |
=(2x0+
| π |
| 3 |
| 1 |
| 2 |
即有x=2x0+
| π |
| 3 |
| 1 |
| 2 |
即有x0=
| 1 |
| 2 |
| π |
| 6 |
则有y=
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
由于x∈[-
| π |
| 6 |
| 2π |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
则有sin(
| 1 |
| 2 |
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
则f(x)∈[-
| ||
| 4 |
| 1 |
| 4 |
故答案为:[-
| ||
| 4 |
| 1 |
| 4 |
点评:本题考查新定义的理解和运用,考查向量的加法运算,考查三角函数的图象和性质,考查运算能力,属于中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
函数y=
的定义域( )
| ||
| x |
| A、{x|x≠0} |
| B、(-4,+∞) |
| C、(-4,0)∪(0,+∞) |
| D、[-4,0)∪(0,+∞) |
已知函数f(x)=-
sin(2x+
)+6sinxcosx-2cos2x+1.
(1)写出函数f(x)的最小正周期和对称轴方程;
(2)求f(x)在区间[0,
]的最值以及取得最值时的相应的x的值.
| 2 |
| π |
| 4 |
(1)写出函数f(x)的最小正周期和对称轴方程;
(2)求f(x)在区间[0,
| π |
| 2 |
如图所示,一个空间几何体的正视图和侧视图都是全等的等腰三角形,俯视图是一个圆,那么这个几何体是( )


| A、正方体 | B、圆锥 | C、圆柱 | D、半球 |
阅读下列程序则该程序对应的程序框图(如图)中,①,②两个判断框内要填写的内容分别是( )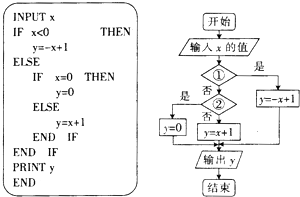

| A、x>0?x<0? |
| B、x>0?x=0 |
| C、x<0?x=0 |
| D、x≥0? x<0 |