题目内容
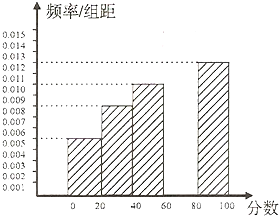 某城市对一项惠民市政工程满意程度(分值:0~100分)进行网上调查,有18000位市民参加了投票,经统计,各分数段的人数如下表:
某城市对一项惠民市政工程满意程度(分值:0~100分)进行网上调查,有18000位市民参加了投票,经统计,各分数段的人数如下表:满意程度
| (分数) | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) |
| 人数K^S*5U.C#O% | 1800 | 2880 | 3600 | 5400 | 4320 |
(Ⅰ)求n的值,并补充完整右边的频率分布直方图;
(Ⅱ)若满意程度在[0,20)的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求至少有一位女性市民被选中的概率.
考点:列举法计算基本事件数及事件发生的概率,频率分布直方图
专题:概率与统计
分析:(1)由分层抽样易得n=50,可得满意程度[0,20)所对应的
=0.015,可补充完整频率分布直方图;
(2)由题意可得满意程度[0,20)投票的5名市民中恰有女性2人,男性3人,用a、b表示女性市民,用1、2、3表示男性市民,列举可得总的基本事件共10个,其中至少有一位女性市民被选中的有7个,由概率公式可得.
| 频率 |
| 组距 |
(2)由题意可得满意程度[0,20)投票的5名市民中恰有女性2人,男性3人,用a、b表示女性市民,用1、2、3表示男性市民,列举可得总的基本事件共10个,其中至少有一位女性市民被选中的有7个,由概率公式可得.
解答:
解:(1)采用分层抽样的方法,样本容量与总体容量的比为
,
∴满意程度[0,20)投票的市民中随机抽取为
×1800=5,解得n=50,
∴满意程度[0,20)所对应的
=0.015,
补充完整频率分布直方图如图所示;

(2)由题意可得满意程度[0,20)投票的5名市民中恰有女性2人,男性3人,
用a、b表示女性市民,用1、2、3表示男性市民,
则总的基本事件为(a,b),(a,1),(a,2),(a,3),(b,1),
(b,2),(b,3),(1,2),(1,3),(2,3)共10个,
其中至少有一位女性市民被选中包含(a,b),(a,1),(a,2),
(a,3),(b,1),(b,2),(b,3),共7个,
∴所求事件的概率为P=
| n |
| 18000 |
∴满意程度[0,20)投票的市民中随机抽取为
| n |
| 18000 |
∴满意程度[0,20)所对应的
| 频率 |
| 组距 |
补充完整频率分布直方图如图所示;

(2)由题意可得满意程度[0,20)投票的5名市民中恰有女性2人,男性3人,
用a、b表示女性市民,用1、2、3表示男性市民,
则总的基本事件为(a,b),(a,1),(a,2),(a,3),(b,1),
(b,2),(b,3),(1,2),(1,3),(2,3)共10个,
其中至少有一位女性市民被选中包含(a,b),(a,1),(a,2),
(a,3),(b,1),(b,2),(b,3),共7个,
∴所求事件的概率为P=
| 7 |
| 10 |
点评:本题考查列举法计算计算事件即事件发生的概率,涉及频率分布直方图,属中档题.

练习册系列答案
相关题目
在平行四边形ABCD中,对角线AC与BD交于点O,若
+
=λ
,则λ的值为( )
| AB |
| AD |
| AO |
| A、2 | ||
| B、1 | ||
C、
| ||
| D、-1 |
下列四个结论:
①若x>0,则x>sinx恒成立;
②命题“若x-sinx=0,则x=0”的逆否命题为“若x≠0,则x-sinx≠0”;
③“命题p∨q为真”是“命题p∧q为真”的充分不必要条件;
④命题“?x∈R,x-lnx>0”的否定是“?x0∈R,x0-lnx0≤0”.
其中正确结论的个数是( )
①若x>0,则x>sinx恒成立;
②命题“若x-sinx=0,则x=0”的逆否命题为“若x≠0,则x-sinx≠0”;
③“命题p∨q为真”是“命题p∧q为真”的充分不必要条件;
④命题“?x∈R,x-lnx>0”的否定是“?x0∈R,x0-lnx0≤0”.
其中正确结论的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
设坐标原点为O,抛物线y2=2x与过焦点的直线交于A、B两点,则
•
等于( )
| OA |
| OB |
A、
| ||
B、-
| ||
| C、3 | ||
| D、-3 |