题目内容
已知点A(-1,2),B(2,5),C(1,7)
(1)求AB边上高线所在直线方程
(2)求BC边上中垂线所在直线方程
(3)求AC边中线所在直线方程.
(1)求AB边上高线所在直线方程
(2)求BC边上中垂线所在直线方程
(3)求AC边中线所在直线方程.
考点:直线的一般式方程与直线的垂直关系,直线的两点式方程
专题:直线与圆
分析:(1)由已知条件先求出直线AB的斜率,利用直线垂直的性质求出AB边上高线所在直线方程的斜率,再由AB边上高线过点C(1,7),能求出AB边上高线所在直线方程.
(2)由已知条件求出线段BC的中点D和BC的斜率,再由直线垂直的性质求出BC边上中垂线所在直线方程的斜率,由BC边上的中垂线过点D,能求出BC边上中垂线所在直线方程.
(3)由已知条件求出线段AC的中点E,由AC边中线所在直线方程过点B,E,利用两点式方程能求出AC边中线所在直线方程.
(2)由已知条件求出线段BC的中点D和BC的斜率,再由直线垂直的性质求出BC边上中垂线所在直线方程的斜率,由BC边上的中垂线过点D,能求出BC边上中垂线所在直线方程.
(3)由已知条件求出线段AC的中点E,由AC边中线所在直线方程过点B,E,利用两点式方程能求出AC边中线所在直线方程.
解答:
解:(1)∵A(-1,2),B(2,5),C(1,7),
∴kAB=
=1,
∴AB边上高线所在直线方程的斜率k1=-
=-1,且过点C(1,7),
∴AB边上高线所在直线方程为:y-7=-(x-1),整理,得:x+y-8=0.
(2)∵A(-1,2),B(2,5),C(1,7),
∴线段BC的中点D(
,6),kBC=
=-2,
∴BC边上中垂线所在直线方程的斜率k2=-
=
,且过点D(
,6),
∴BC边上中垂线所在直线方程为:y-6=
(x-
),整理得2x-4y+21=0.
(3)∵A(-1,2),B(2,5),C(1,7),
∴线段AC的中点E(0,
),
∴AC边中线所在直线方程过点B(2,5),E(0,
),
∴AC边中线所在直线方程为
=
,整理,得x-4y+18=0.
∴kAB=
| 5-2 |
| 2-(-1) |
∴AB边上高线所在直线方程的斜率k1=-
| 1 |
| kAB |
∴AB边上高线所在直线方程为:y-7=-(x-1),整理,得:x+y-8=0.
(2)∵A(-1,2),B(2,5),C(1,7),
∴线段BC的中点D(
| 3 |
| 2 |
| 7-5 |
| 1-2 |
∴BC边上中垂线所在直线方程的斜率k2=-
| 1 |
| kBC |
| 1 |
| 2 |
| 3 |
| 2 |
∴BC边上中垂线所在直线方程为:y-6=
| 1 |
| 2 |
| 3 |
| 2 |
(3)∵A(-1,2),B(2,5),C(1,7),
∴线段AC的中点E(0,
| 9 |
| 2 |
∴AC边中线所在直线方程过点B(2,5),E(0,
| 9 |
| 2 |
∴AC边中线所在直线方程为
| y-5 |
| x-2 |
| ||
| 0-2 |
点评:本题考查直线方程的求法,涉及到直线垂直、中位坐标公式、点斜式方程、两点式方程等知识点的合理运用,是基础题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
已知实数x、y满足
,则z=2x+y的最小值是( )
|
| A、-3 | B、2 | C、0 | D、1 |
函数f(x)=x2ln|x|的图象大致是( )
A、 |
B、 |
C、 |
D、 |
如果a>b,则下列各式正确的是( )
| A、a•2x>b•2x |
| B、ax2>bx2 |
| C、a2>b2 |
| D、a•lgx>b•lgx |
若随机变量X~N(1,4),P(x≤0)=0.1,则P(0<x<2)=( )
| A、0.4 | B、0.45 |
| C、0.8 | D、0.9 |
不等式ln2x+lnx<0的解集是 ( )
| A、(e-1,1) |
| B、(1,e) |
| C、(0,1) |
| D、(0,e-1) |
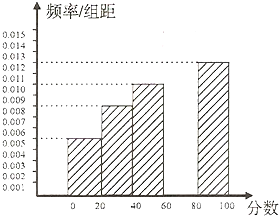 某城市对一项惠民市政工程满意程度(分值:0~100分)进行网上调查,有18000位市民参加了投票,经统计,各分数段的人数如下表:
某城市对一项惠民市政工程满意程度(分值:0~100分)进行网上调查,有18000位市民参加了投票,经统计,各分数段的人数如下表: