题目内容
设坐标原点为O,抛物线y2=2x与过焦点的直线交于A、B两点,则
•
等于( )
| OA |
| OB |
A、
| ||
B、-
| ||
| C、3 | ||
| D、-3 |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据抛物线的标准方程,求出焦点F(
,0 ),当AB的斜率不存在时,可得A(
,1),B(
,-1),求得
•
的值,结合填空题的特点,得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| OA |
| OB |
解答:
解:抛物线y2=2x的焦点F(
,0 ),
当AB的斜率不存在时,可得A(
,1),B(
,-1),
∴
•
=(
,1)•(
,-1)=
-1=-
,
故选:B.
| 1 |
| 2 |
当AB的斜率不存在时,可得A(
| 1 |
| 2 |
| 1 |
| 2 |
∴
| OA |
| OB |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
故选:B.
点评:本题考查抛物线的标准方程,以及简单性质的应用,两个向量的数量积公式,通过给变量取特殊值,检验所给的选项,是一种简单有效的方法.

练习册系列答案
相关题目
如果a>b,则下列各式正确的是( )
| A、a•2x>b•2x |
| B、ax2>bx2 |
| C、a2>b2 |
| D、a•lgx>b•lgx |
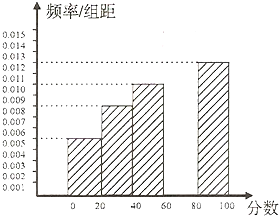 某城市对一项惠民市政工程满意程度(分值:0~100分)进行网上调查,有18000位市民参加了投票,经统计,各分数段的人数如下表:
某城市对一项惠民市政工程满意程度(分值:0~100分)进行网上调查,有18000位市民参加了投票,经统计,各分数段的人数如下表: