题目内容
下列四个结论:
①若x>0,则x>sinx恒成立;
②命题“若x-sinx=0,则x=0”的逆否命题为“若x≠0,则x-sinx≠0”;
③“命题p∨q为真”是“命题p∧q为真”的充分不必要条件;
④命题“?x∈R,x-lnx>0”的否定是“?x0∈R,x0-lnx0≤0”.
其中正确结论的个数是( )
①若x>0,则x>sinx恒成立;
②命题“若x-sinx=0,则x=0”的逆否命题为“若x≠0,则x-sinx≠0”;
③“命题p∨q为真”是“命题p∧q为真”的充分不必要条件;
④命题“?x∈R,x-lnx>0”的否定是“?x0∈R,x0-lnx0≤0”.
其中正确结论的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:命题的真假判断与应用
专题:阅读型,函数的性质及应用,简易逻辑
分析:令y=x-sinx,求出导数,判断单调性,即可判断①;由命题的逆否命题,先将体积、结论调换,再分别对它们否定,即可判断②;由命题p∨q为真,则p,q中至少有一个为真,不能推出p∧q为真,即可判断③;由全称性命题的否定为存在性命题,即可判断④.
解答:
解:对于①,令y=x-sinx,则y′=1-cosx≥0,则有函数y=x-sinx在R上递增,
则当x>0时,x-sinx>0-0=0,则x>sinx恒成立.则①对;
对于②,命题“若x-sinx=0,则x=0”的逆否命题为“若x≠0,则x-sinx≠0”,则②对;
对于③,命题p∨q为真,则p,q中至少有一个为真,不能推出p∧q为真,反之成立,
则应为必要不充分条件,则③错;
对于④,命题“?x∈R,x-lnx>0”的否定是“?x0∈R,x0-lnx0≤0”.则④对.
综上可得,其中正确的叙述共有3个.
故选C.
则当x>0时,x-sinx>0-0=0,则x>sinx恒成立.则①对;
对于②,命题“若x-sinx=0,则x=0”的逆否命题为“若x≠0,则x-sinx≠0”,则②对;
对于③,命题p∨q为真,则p,q中至少有一个为真,不能推出p∧q为真,反之成立,
则应为必要不充分条件,则③错;
对于④,命题“?x∈R,x-lnx>0”的否定是“?x0∈R,x0-lnx0≤0”.则④对.
综上可得,其中正确的叙述共有3个.
故选C.
点评:本题考查函数的单调性的运用,考查复合命题的真假和真值表的运用,考查充分必要条件的判断和命题的否定,属于基础题和易错题.

练习册系列答案
相关题目
函数f(x)=x2ln|x|的图象大致是( )
A、 |
B、 |
C、 |
D、 |
若随机变量X~N(1,4),P(x≤0)=0.1,则P(0<x<2)=( )
| A、0.4 | B、0.45 |
| C、0.8 | D、0.9 |
设x,y满足约束条件
,则z=x-2y的最小值是( )
|
| A、-4 | B、-6 | C、-8 | D、-10 |
“2b=a+c“是“a,b,c成等差数列”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、即不充分也不必要条件 |
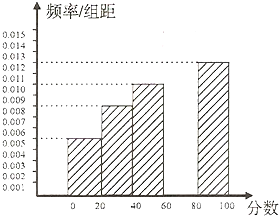 某城市对一项惠民市政工程满意程度(分值:0~100分)进行网上调查,有18000位市民参加了投票,经统计,各分数段的人数如下表:
某城市对一项惠民市政工程满意程度(分值:0~100分)进行网上调查,有18000位市民参加了投票,经统计,各分数段的人数如下表: