题目内容
若等比数列{an}的各项均为正数，且a10a11+a9a12=2e5，则lna1+lna2+…lna20= ．
考点：等比数列的性质,对数的运算性质
专题：等差数列与等比数列
分析：直接由等比数列的性质结合已知得到a10a11=e5，然后利用对数的运算性质化简后得答案．
解答：
解：∵数列{an}为等比数列，且a10a11+a9a12=2e5，
∴a10a11+a9a12=2a10a11=2e5，
则a10a11=e5，
∴lna1+lna2+…lna20=ln(a1a2…a20)=ln(a10a11)10
=ln（e5）10=lne50=50．
故答案为：50．
∴a10a11+a9a12=2a10a11=2e5，
则a10a11=e5，
∴lna1+lna2+…lna20=ln(a1a2…a20)=ln(a10a11)10
=ln（e5）10=lne50=50．
故答案为：50．
点评：本题考查了等比数列的运算性质，考查对数的运算性质，考查了计算能力，是基础题．
练习册系列答案
相关题目
如果若干个函数的图象经过平移后能够重合，则称这些函数为“同簇函数”．给出下列函数：
①f（x）=sinxcosx，
②f（x）=
sin2x+2，
③f（x）=2sin（x+
），
④f（x）=sinx-
cosx，
其中属于“同簇函数”的是（ ）
①f（x）=sinxcosx，
②f（x）=
| 2 |
③f（x）=2sin（x+
| π |
| 4 |
④f（x）=sinx-
| 3 |
其中属于“同簇函数”的是（ ）
| A、①② | B、①④ | C、②③ | D、③④ |
已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2-3x，则函数g（x）=f（x）-x+3的零点的集合为（ ）
| A、{1，3} | ||
| B、{-3，-1，1，3} | ||
C、{2-
| ||
D、{-2-
|
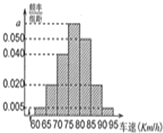2014年“五一节”期间，高速公路车辆较多，交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度，采用的方法是：按到达监控点先后顺序，每隔50辆抽取一辆，总共抽取120辆，分别记下其行车速度，将行车速度（km/h）分成七段[60，65），[65，70），[70，75），[75，80），[80，85），[85，90），[90，95）后得到如图所示的频率分布直方图，据图解答下列问题：