题目内容
10.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{2}$=1,其双曲线的右焦点与抛物线y2=4$\sqrt{3}$x的焦点重合,则该双曲线的方程为${x}^{2}-\frac{{y}^{2}}{2}$=1.分析 由抛物线y2=4$\sqrt{3}$x的焦点为:($\sqrt{3}$,0)可得所求的双曲线c=$\sqrt{3}$,根据a2=c2-b2可求a的值,从而可得双曲线的方程为.
解答 解:∵抛物线y2=4$\sqrt{3}$x的焦点为:($\sqrt{3}$,0)
∴所求的双曲线的右焦点为($\sqrt{3}$,0),故c=$\sqrt{3}$
根据双曲线的定义可知,a2=c2-b2=1
则双曲线的方程为:${x}^{2}-\frac{{y}^{2}}{2}$=1
故答案为:${x}^{2}-\frac{{y}^{2}}{2}$=1.
点评 本题以抛物线的焦点的求解为切入点,主要考查了双曲线的方程的求解,比较基础.

练习册系列答案
相关题目
1.若f(x)=$\frac{x}{x+1}$,f1(x)=f(x),fn(x)=fn-1[f(x)](n≥2,n∈N*),则f(1)+f(2)+…f(2011)+f1(1)+f2(1)+f3(1)…f2011(1)=( )
| A. | 2009 | B. | 2010 | C. | 2011 | D. | 1 |
18.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的右焦点为F,点B是虚轴的一个端点,线段BF与双曲线C的右支交于点A,若$\overrightarrow{BA}=2\overrightarrow{AF}$,则双曲线C的离心率( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{3}{2}$ |
5.某几何体的三视图如图所示,当xy最大时,该几何体外接球的表面积为( )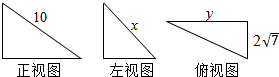

| A. | 32π | B. | 64π | C. | 128π | D. | 136π |
15.设S是由任意n≥5个人组成的集合,如果S中任意4个人当中都至少有1个人认识其余3个人,那么,下面的判断中正确的是( )
| A. | S中没有人认识S中所有的人 | B. | S中至多有2人认识S中所有的人 | ||
| C. | S中至多有2人不认识S中所有的人 | D. | S中至少有1人认识S中的所有人 |
2.已知椭圆的两个焦点为F1(-$\sqrt{5}$,0),F2($\sqrt{5}$,0),M是椭圆上一点,若MF1⊥MF2,|MF1||MF2|=8,则该椭圆的方程是( )
| A. | $\frac{{x}^{2}}{7}$+$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{7}$=1 | C. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1 |