题目内容
11．以下命题中：①设有一个回归方程$\widehat{y}$=2-3x，变量x增加一个单位时，y平均增加3个单位；
②两个随机变量的线性相关性越强，则相关系数的绝对值越接近于1；
③在某项测量中，测量结果ξ服从正态分布N（1，σ2）（σ＞0）．若ξ在（0，1）内取值的概率为0.4，则ξ在（0，2）内取值的概率为0.8．
④将八进制数135（8）转化为二进制数是1011101（2）
其中真命题的个数为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 ①根据回归方程的性质进行判断．
②根据线性相关系数进行判断．
③根据正态分布的性质进行求解判断．
④根据八进制和二进制之间的关系进行判断即可．
解答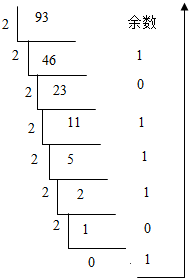 
解：①设有一个回归方程$\widehat{y}$=2-3x，变量x增加一个单位时，y平均减少3个单位，故①错误；
②根据线性相关系数r的意义可知，当两个随机变量线性相关性越强，r的绝对值越接近于1，故②正确；
③在某项测量中，测量结果ξ服从正态分布N（1，σ2）（σ＞0）．若ξ在（0，1）内取值的概率为0.4，
则ξ在（0，2）内取值的概率P=2×0.4=0.8．故③正确，
④将八进制数135（8）转化为10进制数，
135（8）=1×82+3×81+5×80=93（10）．
利用“除2取余法”可得
93（10）=1011101（2）．故④正确，
故真命题的个数为3个，
故选：C
点评 本题考查抽样方法的概念、相关系数的意义以及正态分布的特点和曲线表示的意义，涉及的知识点较多，比较综合．
练习册系列答案
相关题目
1．若f（x）=$\frac{x}{x+1}$，f1（x）=f（x），fn（x）=fn-1[f（x）]（n≥2，n∈N*），则f（1）+f（2）+…f（2011）+f1（1）+f2（1）+f3（1）…f2011（1）=（ ）
| A． | 2009 | B． | 2010 | C． | 2011 | D． | 1 |
2．已知椭圆的两个焦点为F1（-$\sqrt{5}$，0），F2（$\sqrt{5}$，0），M是椭圆上一点，若MF1⊥MF2，|MF1||MF2|=8，则该椭圆的方程是（ ）
| A． | $\frac{{x}^{2}}{7}$+$\frac{{y}^{2}}{2}$=1 | B． | $\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{7}$=1 | C． | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1 | D． | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1 |
16．水平放置的矩形ABCD，长AB=4，宽BC=2，以AB、AD为轴作出斜二测直观图A′B′C′D′，则四边形A′B′C′D′的面积为（ ）
| A． | 4$\sqrt{2}$ | B． | 2$\sqrt{2}$ | C． | 4 | D． | 2 |
3．已知函数f（x）=$\left\{\begin{array}{l}-{x^2}-2x（x≥0）\\{x^2}-2x（x＜0）\end{array}$，又α，β为锐角三角形两锐角则（ ）
| A． | f（sinα）＞f（cosβ） | B． | f（sinα）＜f（cosβ） | C． | f（sinα）＞f（sinβ） | D． | f（cosα）＞f（cosβ） |