题目内容
下列命题中,真命题是( )
| A、?φ∈R,函数y=sin(2x+φ)都不是偶函数 |
| B、?x∈R,使得e2x+3ex+1=0 |
| C、?x0∈R,使得x02≤x0成立 |
| D、“?x∈R,使2x>3”的否定是“?x∈R,使2x≤3” |
考点:命题的真假判断与应用
专题:阅读型,简易逻辑
分析:A.若φ=
,则y=sin(2x+
)=cos2x,即可判断;B.令ex=t(t>0),转化为二次方程,求解即可判断;
C.比如x0=0.5,则0.52<0.5,即可判断;D.由存在性命题的否定是全称性命题,即可判断.
| π |
| 2 |
| π |
| 2 |
C.比如x0=0.5,则0.52<0.5,即可判断;D.由存在性命题的否定是全称性命题,即可判断.
解答:
解:A.若φ=
,则y=sin(2x+
)=cos2x,函数为偶函数,故A错;
B.令ex=t(t>0),则t2+3t+1=0,t=
,故方程无实数解,故B错;
C.比如x0=0.5,则0.52<0.5,故C对;
D.“?x∈R,使2x>3”的否定是“?x∈R,使2x≤3”,故D错.
故选:C.
| π |
| 2 |
| π |
| 2 |
B.令ex=t(t>0),则t2+3t+1=0,t=
-3±
| ||
| 2 |
C.比如x0=0.5,则0.52<0.5,故C对;
D.“?x∈R,使2x>3”的否定是“?x∈R,使2x≤3”,故D错.
故选:C.
点评:本题考查存在性命题和全称性命题的真假,注意运用赋值法和反例,同时考查命题的否定,属于基础题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
△ABC中,若a2-b2=
bc,sinC=2
sinB,则A=( )
| 3 |
| 3 |
| A、150° | B、60° |
| C、120° | D、30° |
已知集合A={y|y=2x},B={y|y=log2x},则A与B的关系是( )
| A、A=B | B、A∩B=∅ |
| C、A?B | D、A⊆B |
一个简单几何体的正视图、俯视图如图所示,则其侧视图不可能是( )
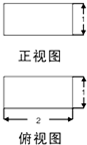

| A、正方形 | B、直角梯形 |
| C、等腰三角形 | D、圆 |
设集合M={x|x>1},N={x|x2>1},则下列关系中正确的是( )
| A、M=N | B、M∪N=N |
| C、M∪N=M | D、M∩N=N |
设随机变量ξ服从正态分布N(0,1),P(ξ>1)=p,则P(-1<ξ<0)等于( )
A、
| ||
| B、1-p | ||
| C、1-2p | ||
D、
|