题目内容
一个简单几何体的正视图、俯视图如图所示，则其侧视图不可能是（ ）
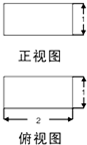
| A、正方形 | B、直角梯形 |
| C、等腰三角形 | D、圆 |
考点：简单空间图形的三视图
专题：空间位置关系与距离
分析：根据空间几何体的三视图，举出几何体为一个圆柱，几何体为一个正四棱柱柱，几何体为一个三柱柱，底面的底边长为高相等的例子，分析它们侧视图的形状，利用排除法可得答案．
解答：
解：若几何体为一个圆柱，则正视图、俯视图如图所示时，侧视图为圆，可排除D；
若几何体为一个正四棱柱柱，则正视图、俯视图如图所示时，侧视图为正方形，可排除A；
若几何体为一个三柱柱，底面的底边长为高相等，则正视图、俯视图如图所示时，侧视图为等腰三角形，可排除C，
故其侧视图不可能是直角梯形，
故选：B
若几何体为一个正四棱柱柱，则正视图、俯视图如图所示时，侧视图为正方形，可排除A；
若几何体为一个三柱柱，底面的底边长为高相等，则正视图、俯视图如图所示时，侧视图为等腰三角形，可排除C，
故其侧视图不可能是直角梯形，
故选：B
点评：本题考查的知识点是简单空间图形的三视图，熟练掌握基本空间图形的三视图形状是解答的关键．
练习册系列答案
相关题目
下列命题中，真命题是（ ）
| A、?φ∈R，函数y=sin（2x+φ）都不是偶函数 |
| B、?x∈R，使得e2x+3ex+1=0 |
| C、?x0∈R，使得x02≤x0成立 |
| D、“?x∈R，使2x＞3”的否定是“?x∈R，使2x≤3” |
已知集合M={1，2，3，5}，N={x|x=2k-1，k∈M}，则M∩N=（ ）
| A、{1，2，3} |
| B、{1，3，5} |
| C、{2，3，5} |
| D、M |
满足性质f（x+y）=f（x）+f（y）的函数是（ ）
| A、f（x）=3x |
| B、f（x）=3x+1 |
| C、f（x）=x2 |
| D、f（x）=3|x| |
设m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题正确的是（ ）
| A、若m?β，α⊥β，则m⊥α |
| B、若α∥β，m?α，n?β，则m∥n |
| C、若n⊥α，n⊥β，m⊥α，则m⊥β |
| D、若α⊥γ，β⊥γ，m⊥α，则m⊥β |
如图是函数f（x）=Asin（ωx+φ）（x∈R）在区间[| π |
| 6 |
| 7π |
| 6 |
A、向右平移
| ||||
B、向右平移
| ||||
C、向左平移
| ||||
D、向左平移
|
x∈[0，2π]，使得sinx≥
成立的x的取值范围是（ ）
| 1 |
| 3 |
A、[0，arccos
| ||||||||||
B、[arccos
| ||||||||||
C、[π-arccos
| ||||||||||
D、[arccos
|