题目内容
6．已知f（x）的定义在R上的奇函数，当x＞0时，f（x）=1+ax（a＞0）且a≠1），若f（-1）=-$\frac{3}{2}$，则a=$\frac{1}{2}$．分析 根据条件，得到f（-1）=-f（1）=-1-a=-$\frac{3}{2}$，即可求出a的值．
解答 解：由题意，当x＞0时，f（x）=1+ax（a＞0）且a≠1），f（-1）=-$\frac{3}{2}$，
∴f（-1）=-f（1）=-1-a=-$\frac{3}{2}$，
∴a=$\frac{1}{2}$．
故答案为$\frac{1}{2}$．
点评 本题主要考查了函数奇偶性的性质，以及函数求值，同时考查了计算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
17．将边长为$\sqrt{2}$的正方形ABCD沿对角线AC折成一个直二面角B-AC-D．则四面体ABCD的内切球的半径为（ ）
| A． | 1 | B． | $2\sqrt{2}-\sqrt{3}$ | C． | $\sqrt{2}-1$ | D． | $2-\sqrt{3}$ |
14．
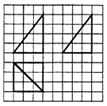如图，网格纸上小正方形的边长为1，粗实线画出的是某四棱锥的三视图，则该四棱锥的外接球的表面积为（ ）
如图，网格纸上小正方形的边长为1，粗实线画出的是某四棱锥的三视图，则该四棱锥的外接球的表面积为（ ）| A． | 136π | B． | 34π | C． | 25π | D． | 18π |
1．已知向量$\overrightarrow{a}$=（3，4），若λ$\overrightarrow{a}$=（3λ，2μ）（λ，μ∈R），且|λ$\overrightarrow{a}$|=5，则λ+μ=（ ）
| A． | 3 | B． | -3 | C． | ±3 | D． | -1 |
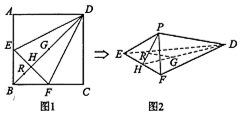如图l，在正方形ABCD中，点E，F分别是AB，BC的中点，BD与EF交于点H，点G，R分别在线段DH，HB上，且$\frac{DG}{GH}$=$\frac{BR}{RH}$．将△AED，△CFD，△BEF分别沿DE，DF，EF折起，使点A，B，C重合于点P，如图2所示，
16．先把函数y=sin（x+φ）的图象上个点的横坐标缩短为原来的$\frac{1}{2}$（纵坐标不变），再向右平移$\frac{π}{3}$个单位，所得函数关于y轴对称，则φ的值可以是（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $-\frac{π}{6}$ | D． | $-\frac{π}{3}$ |