题目内容
11.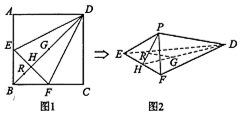 如图l,在正方形ABCD中,点E,F分别是AB,BC的中点,BD与EF交于点H,点G,R分别在线段DH,HB上,且$\frac{DG}{GH}$=$\frac{BR}{RH}$.将△AED,△CFD,△BEF分别沿DE,DF,EF折起,使点A,B,C重合于点P,如图2所示,
如图l,在正方形ABCD中,点E,F分别是AB,BC的中点,BD与EF交于点H,点G,R分别在线段DH,HB上,且$\frac{DG}{GH}$=$\frac{BR}{RH}$.将△AED,△CFD,△BEF分别沿DE,DF,EF折起,使点A,B,C重合于点P,如图2所示,(I)求证:GR⊥平面PEF;
(Ⅱ)若正方形ABCD的边长为4,求三棱锥P-DEF的内切球的半径.
分析 (Ⅰ)推导出PD⊥平面PEF,RG∥PD,由此能证明GR⊥平面PEF.
(Ⅱ)设三棱锥P-DEF的内切球半径为r,由三棱锥的体积V=$\frac{1}{3}({S}_{△PEF}+2{S}_{△DPF}+{S}_{△DEF})•r$,能求出棱锥P-DEF的内切球的半径.
解答 证明:(Ⅰ)在正方形ABCD中,∠A、∠B、∠C均为直角,
∴在三棱锥P-DEF中,PE,PF,PD三条线段两两垂直,
∴PD⊥平面PEF,
∵$\frac{DG}{GH}$=$\frac{BR}{RH}$,即$\frac{DG}{GH}=\frac{PR}{RH}$,∴在△PDH中,RG∥PD,
∴GR⊥平面PEF.
解:(Ⅱ)正方形ABCD边长为4,
由题意PE=PF=2,PD=4,EF=2$\sqrt{2}$,DF=2$\sqrt{5}$,
∴S△PEF=2,S△PFD=S△DPE=4,
${S}_{△DEF}=\frac{1}{2}×2\sqrt{2}×\sqrt{(2\sqrt{5})^{2}-(\sqrt{2})^{2}}$=6,
设三棱锥P-DEF的内切球半径为r,
则三棱锥的体积:
${V}_{P-DEF}=\frac{1}{6}×2×2×4$=$\frac{1}{3}({S}_{△PEF}+2{S}_{△DPF}+{S}_{△DEF})•r$,
解得r=$\frac{1}{2}$,
∴三棱锥P-DEF的内切球的半径为$\frac{1}{2}$.
点评 本题考查线面垂直的证明,考查三棱锥的内切的半径的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
2.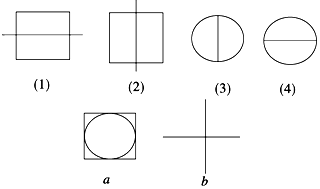 定义A*B,B*C,C*D,D*A的运算分别对应下面图中的(1),(2),(3),(4),则图中,a,b对应的运算是( )
定义A*B,B*C,C*D,D*A的运算分别对应下面图中的(1),(2),(3),(4),则图中,a,b对应的运算是( )
 定义A*B,B*C,C*D,D*A的运算分别对应下面图中的(1),(2),(3),(4),则图中,a,b对应的运算是( )
定义A*B,B*C,C*D,D*A的运算分别对应下面图中的(1),(2),(3),(4),则图中,a,b对应的运算是( )| A. | B*D,A*D | B. | B*D,A*C | C. | B*C,A*D | D. | C*D,A*D |
19.在△ABC中,BC:AB=2:$\sqrt{3}$,∠B=30°,则∠C=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
16.已知α,β,γ是三个不同的平面,l,m是两条不同的直线,则下列命题一定正确的是( )
| A. | 若l丄α,l∥β则 α∥β | |
| B. | 若γ丄α,γ丄β,则 α∥β | |
| C. | 若l∥m且 l?α,m?β,l∥β,m∥α,则 α∥β | |
| D. | 若l,m 异面,且 l?α,m?β,l∥β,m∥α,则 α∥β |