题目内容
求函数y=-3cos2x-4sinx+4,x∈[
,π]的值域.
| π |
| 3 |
考点:三角函数的最值
专题:三角函数的求值
分析:根据x∈[
,π],求得sinx∈[0,1],再根据函数y=3(sinx-
)2-
,利用二次函数的性质求得它的值域.
| π |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
解答:
解:∵x∈[
,π],∴sinx∈[0,1],
∵函数y=-3cos2x-4sinx+4=3sin2x-4sinx+1=3(sinx-
)2-
,
故当sinx=
时,函数取得最小值为-
,当sinx=0时,函数取得最大值为1,
故函数的值域为[-
,0].
| π |
| 3 |
∵函数y=-3cos2x-4sinx+4=3sin2x-4sinx+1=3(sinx-
| 2 |
| 3 |
| 1 |
| 3 |
故当sinx=
| 2 |
| 3 |
| 1 |
| 3 |
故函数的值域为[-
| 1 |
| 3 |
点评:本题主要考查正弦函数的定义域和值域,二次函数的性质,属于中档题.

练习册系列答案
相关题目
设随机变量的分布列如下表所示,且a+2b=1.3,则a-b=( )
| X | 0 | 1 | 2 | 3 |
| P | 0.1 | a | b | 0.1 |
| A、0.5 | B、0.3 |
| C、0.2 | D、-0.2 |
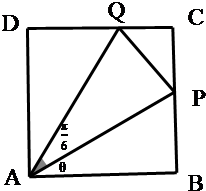 如图,某污水处理厂要在一正方形污水处理池ABCD内修建一个三角形隔离区以投放净化物质,其形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知AB=20米,∠PAQ=
如图,某污水处理厂要在一正方形污水处理池ABCD内修建一个三角形隔离区以投放净化物质,其形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知AB=20米,∠PAQ=