题目内容

已知正数x，y满足3x+4y=xy，则x+3y的最小值为
 
．
考点：基本不等式
专题：不等式的解法及应用
分析：由正数x，y满足3x+4y=xy，可得
3
y
+
4
x
=1．利用“乘1法”与基本不等式的性质即可得出．
解答： 解：由正数x，y满足3x+4y=xy，∴
3
y
+
4
x
=1．
∴x+3y=(x+3y)(
4
x
+
3
y
)=13+
12y
x
+
3x
y
≥13+2
12y
x
×
3x
y
=25，当且仅当x=2y=10时，取等号．
∴x+3y的最小值为25．
故答案为：25．
点评：本题考查了“乘1法”与基本不等式的性质，属于基础题．
练习册系列答案
相关题目
设m，n是两条不同的直线，α，β，γ是两个不同的平面，则下列四个命题中真命题是：
 
．
①若m?β，α⊥β，则m⊥α；
②若α∥β，m?α，则m∥β；
③若n⊥α，n⊥β，m⊥α，则m⊥β；
④若α⊥γ，β⊥γ，则α⊥β．
已知函数f（x）=ln
1+x
1-x
，x1，x2∈（-1，1）．
（1）求证：f（x1）+f（x2）=f（
x1+x2
1+x1x2
）；
（2）若a，b∈（-1，1），且f（
a+b
1+ab
）=1，f（-b）=
1
2
，求f（a）的值．
已知函数f（x）=x2-4x，x∈[1，5），则此函数的值域为（　　）
A、[-4，+∞）
B、[-3，5）
C、[-4，5]
D、[-4，5）
若函数f（x）=
f(x+3)，x＜6
log
1
2
x，x≥6
，则f（-1）的值
 
．
已知集合A={x|a≤x≤a+3}，B={x|x＜3或x＞8}．
（1）当a=2时，求∁R（A∩B），（∁RA）∪B．
（2）若集合A⊆B，求实数a的取值范围．
已知f（x）=ax3-bx+2，且f（-5）=17，则f（5）=
 
．
设有集合A={x|x2-[x]=2}和B={x||x|＜2}，求A∩B和A∪B（其中[x]表示不超过实数x之值的最大整数）
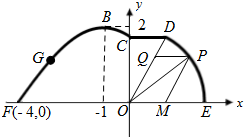如图，在海岸线EF一侧有一休闲游乐场，游乐场的前一部分边界为曲线段FGBC，该曲线段是函数y=Asin（ωx+ϕ）（A＞0，ω＞0，ϕ∈（0，π）），x∈[-4，0]的图象，图象的最高点为B（-1，2）．边界的中间部分为长1千米的直线段CD，且CD∥EF．游乐场的后一部分边界是以O为圆心的一段圆弧
DE
．
（1）求曲线段FGBC的函数表达式；
（2）曲线段FGBC上的入口G距海岸线EF最近距离为1千米，现准备从入口G修一条笔直的景观路到O，求景观路GO长；
（3）如图，在扇形ODE区域内建一个平行四边形休闲区OMPQ，平行四边形的一边在海岸线EF上，一边在半径OD上，另外一个顶点P在圆弧
DE
上，且∠POE=θ，求平行四边形休闲区OMPQ面积的最大值及此时θ的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网