题目内容
已知f（x）=ax3-bx+2，且f（-5）=17，则f（5）= ．
考点：函数奇偶性的性质,函数的值
专题：函数的性质及应用
分析：通过观察f（x）解析式，会发现ax3-bx是奇函数，f（x）-2是奇函数，这样便可由f（-5）的值求出f（5）的值．
解答：
解：f（x）-2=ax3-bx；
∵f（-x）-2=-（ax3-bx）=-（f（x）-2）；
∴函数f（x）-2是奇函数
∴f（-5）-2=-（f（5）-2）=17-2；
∴f（5）=-13．
故答案为：-13．
∵f（-x）-2=-（ax3-bx）=-（f（x）-2）；
∴函数f（x）-2是奇函数
∴f（-5）-2=-（f（5）-2）=17-2；
∴f（5）=-13．
故答案为：-13．
点评：本题考查函数的奇偶性的应用，能判断出f（x）-2是奇函数是解本题的关键．
练习册系列答案
全能测控一本好卷系列答案
相关题目
下列函数是偶函数的是（ ）
| A、y=x | ||
B、y=x
| ||
| C、y=x2，x∈[0，1] | ||
| D、y=2x2-3 |
若复数z满足（3+4i）z=|4-3i|，则复数z对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
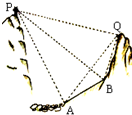如图，为了测量两座山峰上两点P、Q之间的距离，选择山坡上一段长度为300