题目内容
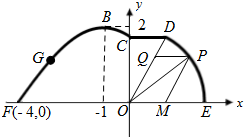 如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数y=Asin(ωx+ϕ)(A>0,ω>0,ϕ∈(0,π)),x∈[-4,0]的图象,图象的最高点为B(-1,2).边界的中间部分为长1千米的直线段CD,且CD∥EF.游乐场的后一部分边界是以O为圆心的一段圆弧
如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数y=Asin(ωx+ϕ)(A>0,ω>0,ϕ∈(0,π)),x∈[-4,0]的图象,图象的最高点为B(-1,2).边界的中间部分为长1千米的直线段CD,且CD∥EF.游乐场的后一部分边界是以O为圆心的一段圆弧 |
| DE |
(1)求曲线段FGBC的函数表达式;
(2)曲线段FGBC上的入口G距海岸线EF最近距离为1千米,现准备从入口G修一条笔直的景观路到O,求景观路GO长;
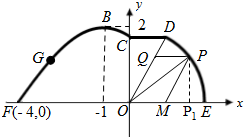
(3)如图,在扇形ODE区域内建一个平行四边形休闲区OMPQ,平行四边形的一边在海岸线EF上,一边在半径OD上,另外一个顶点P在圆弧
 |
| DE |
考点:在实际问题中建立三角函数模型
专题:应用题,函数的性质及应用,三角函数的图像与性质
分析:(1)由题意可得A=2,T=12,代入点求ϕ,从而求解析式;
(2)令y=2sin(
x+
)=1求解x,从而求景观路GO的长;
(3)作图求平行四边形的面积SOMPQ=OM•PP1=(2cosθ-
sinθ)2sinθ=
sin(2θ+
)-
,θ∈(0,
);从而求最值.
(2)令y=2sin(
| π |
| 6 |
| 2π |
| 3 |
(3)作图求平行四边形的面积SOMPQ=OM•PP1=(2cosθ-
2
| ||
| 3 |
4
| ||
| 3 |
| π |
| 6 |
2
| ||
| 3 |
| π |
| 3 |
解答:
解:(1)由已知条件,得A=2,
又∵
=3 ,T=
=12 ,
∴ω=
,
又∵当x=-1时,
有y=2sin(-
+ϕ)=2
∴ ϕ=
,
∴曲线段FBC的解析式为y=2sin(
x+
) ,x∈[-4,0].
(2)由y=2sin(
x+
)=1得,
x=6k+(-1)k-4(k∈Z),
又∵x∈[-4,0],
∴k=0,x=-3,
∴G(-3,1),OG=
;
∴景观路GO长为
千米.
(3)如图,
OC=
,CD=1 ,
∴ OD=2 ,∠COD=
,
作PP1⊥x轴于P1点,在Rt△OPP1中,
PP1=OPsinθ=2sinθ,
在△OMP中,
=
,
∴OM=
=2cosθ-
sinθ,
SOMPQ=OM•PP1=(2cosθ-
sinθ)2sinθ=2sin2θ+
cos2θ-
=
sin(2θ+
)-
,θ∈(0,
);
当2θ+
=
时,即θ=
时,
平行四边形面积有最大值为
(平方千米).
又∵
| T |
| 4 |
| 2π |
| ω |
∴ω=
| π |
| 6 |
又∵当x=-1时,
有y=2sin(-
| π |
| 6 |
∴ ϕ=
| 2π |
| 3 |
∴曲线段FBC的解析式为y=2sin(
| π |
| 6 |
| 2π |
| 3 |
(2)由y=2sin(
| π |
| 6 |
| 2π |
| 3 |
x=6k+(-1)k-4(k∈Z),
又∵x∈[-4,0],
∴k=0,x=-3,
∴G(-3,1),OG=
| 10 |
∴景观路GO长为
| 10 |
(3)如图,

OC=
| 3 |
∴ OD=2 ,∠COD=
| π |
| 6 |
作PP1⊥x轴于P1点,在Rt△OPP1中,
PP1=OPsinθ=2sinθ,
在△OMP中,
| OP |
| sin120° |
| OM |
| sin(60°-θ) |
∴OM=
| OPsin(60°-θ) |
| sin120° |
2
| ||
| 3 |
SOMPQ=OM•PP1=(2cosθ-
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
=
4
| ||
| 3 |
| π |
| 6 |
2
| ||
| 3 |
| π |
| 3 |
当2θ+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
平行四边形面积有最大值为
2
| ||
| 3 |
点评:本题考查了三角函数在实际问题中的应用,同时考查了学生的作图能力,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
设函数fn(x)=x-
+
-…+(-1)n-1
,(x∈[0,1],n∈N*),则( )
| x3 |
| 3! |
| x5 |
| 5! |
| x2n-1 |
| (2n-1)! |
| A、f2(x)≤sinx≤f3(x) |
| B、f3(x)≤sinx≤f2(x) |
| C、sinx≤f2(x)≤f3(x) |
| D、f2(x)≤f3(x)≤sinx |
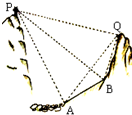 如图,为了测量两座山峰上两点P、Q之间的距离,选择山坡上一段长度为300
如图,为了测量两座山峰上两点P、Q之间的距离,选择山坡上一段长度为300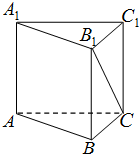 如图,正三棱柱的底面边长为2,体积为
如图,正三棱柱的底面边长为2,体积为