题目内容
已知函数f(x)=|3x-1|+|ax-1|(a>0).
(Ⅰ)当a=2时,求不等式f(x)≥4的解集;
(Ⅱ)若对任意的x∈R,都有f(x)≥f(
),求a的取值范围.
(Ⅰ)当a=2时,求不等式f(x)≥4的解集;
(Ⅱ)若对任意的x∈R,都有f(x)≥f(
| 1 |
| 3 |
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)当a=2时,分类讨论求得不等式f(x)≥4的解集.
(Ⅱ)分当a>3时、当0<a≤3时两种情况,分别利用f(x)的单调性,根据f(x)≥f(
)恒成立,分别求得a的取值范围,再取并集,即得所求.
(Ⅱ)分当a>3时、当0<a≤3时两种情况,分别利用f(x)的单调性,根据f(x)≥f(
| 1 |
| 3 |
解答:
解:(Ⅰ)当a=2时,f(x)=|3x-1|+|2x-1|=
,
当x≥
时,由f(x)=5x-2≥4,得x≥
;
当
<x<
时,由f(x)=x≥4,无解;
当x≤
时,由f(x)=-5x+2≥4,解得x≤-
;
综上可知,f(x)≥4的解集为{x|x≥
或x≤-
}.
(Ⅱ)当a>3时,f(x)=|3x-1|+|ax-1|=
,
故f(x)在区间(-∞,
]上单调递减,在区间[
,+∞)上单调递增.
故f(x)≥f(
),与题意不符.
当0<a≤3时,f(x)=|3x-1|+|ax-1|=
,
故f(x)在区间(-∞,
]上单调递减,在区间[
,+∞)单调递增,故有 f(x)≥f(
),
综上可知,a的取值范围为(0,3].
|
当x≥
| 1 |
| 2 |
| 6 |
| 5 |
当
| 1 |
| 3 |
| 1 |
| 2 |
当x≤
| 1 |
| 3 |
| 2 |
| 5 |
综上可知,f(x)≥4的解集为{x|x≥
| 6 |
| 5 |
| 2 |
| 5 |
(Ⅱ)当a>3时,f(x)=|3x-1|+|ax-1|=
|
故f(x)在区间(-∞,
| 1 |
| a |
| 1 |
| a |
故f(x)≥f(
| 1 |
| a |
当0<a≤3时,f(x)=|3x-1|+|ax-1|=
|
故f(x)在区间(-∞,
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
综上可知,a的取值范围为(0,3].
点评:本题主要考查绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
各大学在高考录取时采取专业志愿优先的录取原则.一考生从某大学所给的7个专业中,选择3个作为自己的第一、二、三专业志愿,其中甲、乙两个专业不能同时兼报,则该考生不同的填报专业志愿的方法有( )
| A、210种 | B、180种 |
| C、120种 | D、95种 |
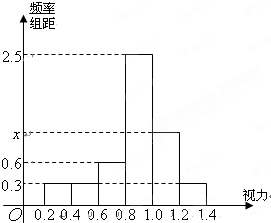 为了解某校高三学生的视力情况,随机抽查了该校50名高三学生,得到如图所示的频率分布直方图.
为了解某校高三学生的视力情况,随机抽查了该校50名高三学生,得到如图所示的频率分布直方图.