题目内容
如图是一个几何体的三视图(单位:cm)求这个几何体的表面积及体积;


考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:几何体可看成是正方体AC1及直三棱柱B1C1Q-A1D1P的组合体,求出底面面积,然后求出体积即可.
解答:
 解:几何体的直观图如图所示.
解:几何体的直观图如图所示.
几何体可看成是正方体AC1及直三棱柱B1C1Q-A1D1P的组合体.
由PA1=PD1=
,A1D1=AD=2,可得PA1⊥PD1.
故所求几何体的表面积
S=5×22+2×
×2×1+2×
×2
=22+4
(cm2),
所求几何体的体积V=23+
×(
)2×2=10(cm3).
 解:几何体的直观图如图所示.
解:几何体的直观图如图所示.几何体可看成是正方体AC1及直三棱柱B1C1Q-A1D1P的组合体.
由PA1=PD1=
| 2 |
故所求几何体的表面积
S=5×22+2×
| 1 |
| 2 |
| 2 |
=22+4
| 2 |
所求几何体的体积V=23+
| 1 |
| 2 |
| 2 |
点评:本题考查三视图复原几何体,画出中逐步按照三视图的作法复原,考查空间想象能力,逻辑推理能力,计算能力,转化思想,是中档题.

练习册系列答案
相关题目
将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
…
按照以上排列的规律,第8行从左向右的第5个数为( )
1
2 3
4 5 6
7 8 9 10
…
按照以上排列的规律,第8行从左向右的第5个数为( )
| A、30 | B、31 | C、32 | D、33 |
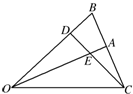 如图所示,已知△AOB中,点C与点B关于点A对称,
如图所示,已知△AOB中,点C与点B关于点A对称,