题目内容
已知函数f(x)=x-alnx,g(x)=
.
(Ⅰ) 若函数f(x)存在不大于0的最小值,求实数a的取值范围;
(Ⅱ)设x=1是函数f(x)的极小值点.
(i)若函数f(x)与函数g(x)的图象分别在直线y=kx的两侧,求k的取值范围;
(ii) 若M(x1,y1),N(x2,y2)(0<x1<x2)是f(x)图象上的两点,且存在实x0∈(0,+∞)
使得f′(x0)=
,证明:x1<x0<x2.
| lnx |
| x |
(Ⅰ) 若函数f(x)存在不大于0的最小值,求实数a的取值范围;
(Ⅱ)设x=1是函数f(x)的极小值点.
(i)若函数f(x)与函数g(x)的图象分别在直线y=kx的两侧,求k的取值范围;
(ii) 若M(x1,y1),N(x2,y2)(0<x1<x2)是f(x)图象上的两点,且存在实x0∈(0,+∞)
使得f′(x0)=
| f(x2)-f(x1) |
| x2-x1 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的极值
专题:导数的综合应用
分析:(I)先求出 f/(x)=1-
=
,x>0,讨论当a≤0,a>0时的情况,从而求出a的范围.
(II)设x=1是函数f(x)的极小值点,由(I)知:f(x)极小值=f(a),从而a=1.
(i)设直线y=kx与函数f(x)的图象相切于点(x1,y1),设直线y=kx与函数g(x)的图象相切于点(x2,y2),得方程组求出k的值,再根据函数的图象进而求出k的范围.
(ii)求出f′(x0)=
,得
=
;由
-
=
-
=
记
=t,h(t)=lnt-t+1,t>1,得h(t)<h(1)=0,进而x1<x0;从而问题得解.
| a |
| x |
| x-a |
| x |
(II)设x=1是函数f(x)的极小值点,由(I)知:f(x)极小值=f(a),从而a=1.
(i)设直线y=kx与函数f(x)的图象相切于点(x1,y1),设直线y=kx与函数g(x)的图象相切于点(x2,y2),得方程组求出k的值,再根据函数的图象进而求出k的范围.
(ii)求出f′(x0)=
| f(x2)-f(x1) |
| x2-x1 |
| 1 |
| x0 |
| lnx2-lnx1 |
| x2-x1 |
| 1 |
| x0 |
| 1 |
| x1 |
| lnx2-lnx1 |
| x2-x1 |
| 1 |
| x1 |
x1(ln
| ||||
| (x2-x1)x1 |
| x2 |
| x1 |
解答:
解:(I)∵f/(x)=1-
=
,x>0;
当a≤0时,函数f(x)在(0,+∞)递增,
∴f(x)不存在最小值;
当a>0时,
由f′(x)≤0,得0<x≤a;
由f′(x)>0,得x>a;
∴函数f(x)在(0,a)递减,在(a,+∞)递增,
∴当x=a时,[f(x)]min=a-alna;
由a-alna≤0,得a≥e;
∴实数a的取值范围为[e,+∞).
(II)∵设x=1是函数f(x)的极小值点,
由(I)知:f(x)极小值=f(a),
∴a=1.
(i)设直线y=kx与函数f(x)的图象相切于点(x1,y1),
则
解得k=1-
;
设直线y=kx与函数g(x)的图象相切于点(x2,y2),
∵g/(x)=
,
则
解得k=
;
∵函数f(x)与函数g(x)的图象分别在直线y=kx的两侧(如图示),
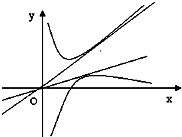 ,
,
∴k的取值范围为(1-
,
).
(ii)∵f′(x0)=
,
∴1-
=
,
∴
=
;
∵
-
=
-
=
又∵0<x1<x2,
∴(x2-x1)x1>0;
记
=t,h(t)=lnt-t+1,t>1,
∵h/(t)=
-1<0,
∴h(t)在(1,+∞)递减,
∴h(t)<h(1)=0,
即
-
<0⇒
<
,
∴x1<x0;
同理∴x0<x2,
∴x1<x0<x2.
| a |
| x |
| x-a |
| x |
当a≤0时,函数f(x)在(0,+∞)递增,
∴f(x)不存在最小值;
当a>0时,
由f′(x)≤0,得0<x≤a;
由f′(x)>0,得x>a;
∴函数f(x)在(0,a)递减,在(a,+∞)递增,
∴当x=a时,[f(x)]min=a-alna;
由a-alna≤0,得a≥e;
∴实数a的取值范围为[e,+∞).
(II)∵设x=1是函数f(x)的极小值点,
由(I)知:f(x)极小值=f(a),
∴a=1.
(i)设直线y=kx与函数f(x)的图象相切于点(x1,y1),
则
|
| 1 |
| e |
设直线y=kx与函数g(x)的图象相切于点(x2,y2),
∵g/(x)=
| 1-lnx |
| x2 |
则
|
| 1 |
| 2e |
∵函数f(x)与函数g(x)的图象分别在直线y=kx的两侧(如图示),
 ,
,∴k的取值范围为(1-
| 1 |
| e |
| 1 |
| 2e |
(ii)∵f′(x0)=
| f(x2)-f(x1) |
| x2-x1 |
∴1-
| 1 |
| x0 |
| (x2-lnx2)-(x1-lnx1) |
| x2-x1 |
∴
| 1 |
| x0 |
| lnx2-lnx1 |
| x2-x1 |
∵
| 1 |
| x0 |
| 1 |
| x1 |
| lnx2-lnx1 |
| x2-x1 |
| 1 |
| x1 |
x1(ln
| ||||
| (x2-x1)x1 |
又∵0<x1<x2,
∴(x2-x1)x1>0;
记
| x2 |
| x1 |
∵h/(t)=
| 1 |
| t |
∴h(t)在(1,+∞)递减,
∴h(t)<h(1)=0,
即
| 1 |
| x0 |
| 1 |
| x1 |
| 1 |
| x0 |
| 1 |
| x1 |
∴x1<x0;
同理∴x0<x2,
∴x1<x0<x2.
点评:本题考查三角恒等变化、三角函数的图象与性质、零点与方程的根、数学归纳法等基础知识,考查运算求解能力、推理论证能力,考查数形结合思想、函数与方程思想、特殊与一般思想等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 如图,C岛位于我南海A港口北偏东60方向,距A港口60
如图,C岛位于我南海A港口北偏东60方向,距A港口60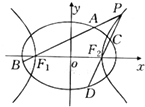 如图,已知以F1(-2,0),F2(2,0)为焦点的椭圆上有点Q,三角形QF1F2的周长为4(
如图,已知以F1(-2,0),F2(2,0)为焦点的椭圆上有点Q,三角形QF1F2的周长为4(