题目内容
如图,边长为2的菱形ABCD中,∠ABC=60°,点E,F分别是AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.

(1)求证:A′D⊥EF;
(2)求二面角A′-EF-D的余弦值.

(1)求证:A′D⊥EF;
(2)求二面角A′-EF-D的余弦值.
考点:与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
分析:(1)取EF的中点O,连结OD,OA',证明EF⊥平面A'OD,即可证明A′D⊥EF;
(2)证明∠A'OD是二面角A'-EF-D的平面角,利用余弦定理,即可求二面角A′-EF-D的余弦值.
(2)证明∠A'OD是二面角A'-EF-D的平面角,利用余弦定理,即可求二面角A′-EF-D的余弦值.
解答:
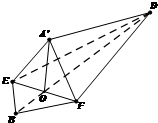 (1)证明:取EF的中点O,连结OD,OA',
(1)证明:取EF的中点O,连结OD,OA',
因为DE=DF,A'E=A'F,
所以EF⊥OA',EF⊥OD,
因为OA'∩OD=O,
所以EF⊥平面A'OD,…(3分)
因为A'D?平面A'EF,
所以A'D⊥EF…(4分)
(2)解:由已知,EF⊥OA',EF⊥OD,
所以∠A'OD是二面角A'-EF-D的平面角.…(5分)
因为OD=
,OA′=
,A′D=2.
所以cos∠A′OD=
=
.
所以所求角的余弦值为
.…(8分)
 (1)证明:取EF的中点O,连结OD,OA',
(1)证明:取EF的中点O,连结OD,OA',因为DE=DF,A'E=A'F,
所以EF⊥OA',EF⊥OD,
因为OA'∩OD=O,
所以EF⊥平面A'OD,…(3分)
因为A'D?平面A'EF,
所以A'D⊥EF…(4分)
(2)解:由已知,EF⊥OA',EF⊥OD,
所以∠A'OD是二面角A'-EF-D的平面角.…(5分)
因为OD=
3
| ||
| 2 |
| ||
| 2 |
所以cos∠A′OD=
| ||||||||
2•
|
| 7 |
| 9 |
所以所求角的余弦值为
| 7 |
| 9 |
点评:本题考查线面垂直的判定,考查面面角,考查学生分析解决问题的能力,正确运用线面垂直的判定是关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目

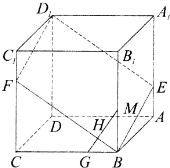 如图,已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,且AE=F1C=1.
如图,已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,且AE=F1C=1.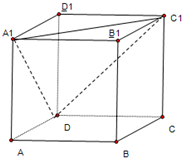 在正方体ABCD-A1B1C1D1中,求平面A1DC1与平面ADD1A1所成角的正切值.
在正方体ABCD-A1B1C1D1中,求平面A1DC1与平面ADD1A1所成角的正切值.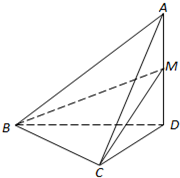 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2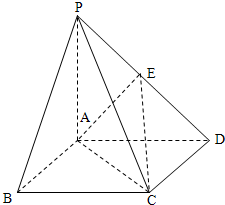 如图,在四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥面ABCD,且PA=AB=4,E为PD中点.
如图,在四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥面ABCD,且PA=AB=4,E为PD中点.