题目内容
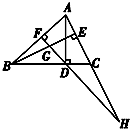如图，AD、BE是△ABC的高，DF⊥AB于F，DF交BE于G，FD的延长线交AC的延长线于H，求证：DF2=FG•FH．考点：相似三角形的性质
专题：立体几何
分析：由已知条件，推导出△BFG∽△HFA，从而得到BF•AF=FG•HF，在Rt△ADB中，DF2=BF•AF，由此能够证明DF2=FG•FH．
解答：
证明：∵BE⊥AC，∴∠ABE+∠BAE=90°，
∵DF⊥AB，∴∠AHF+∠BAE=90°，
∴∠ABE=∠H，
又∵∠BFG=∠HFA=90°，
△BFG∽△HFA，
∴
=
，
∴BF•AF=FG•HF，
在Rt△ADB中，DF2=BF•AF，
∴DF2=FG•FH．
∵DF⊥AB，∴∠AHF+∠BAE=90°，
∴∠ABE=∠H，
又∵∠BFG=∠HFA=90°，
△BFG∽△HFA，
∴
| BF |
| HF |
| FG |
| AF |
∴BF•AF=FG•HF，
在Rt△ADB中，DF2=BF•AF，
∴DF2=FG•FH．
点评：本题考查相似三角形的性质的应用，是中档题，解题时要注意等价转化思想的合理运用．
练习册系列答案
灵星计算小达人系列答案
相关题目
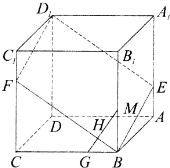如图，已知ABCD-A1B1C1D1是棱长为3的正方体，点E在AA1上，点F在CC1上，且AE=F1C=1．
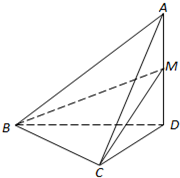如图，在四面体A-BCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2
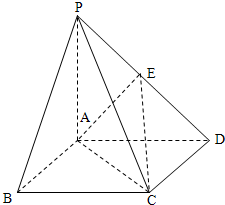如图，在四棱锥P-ABCD中，四边形ABCD为正方形，PA⊥面ABCD，且PA=AB=4，E为PD中点．
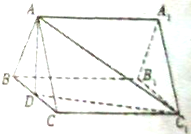如图，在三棱柱ABC-A1B1C1中，底面ABC是边长为2的正三角形，侧棱长为2，且侧棱AA1⊥底面ABC，点D是BC的中点
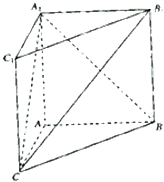如图，在直三棱柱ABC-A1B1C1中，