题目内容
15.设离散型随机变量X~N(0,1),则P(X≤0)=0.5;P(-2<X≤2)=0.9544.分析 根据正态分布的对称性得出答案.
解答 解:∵X~N(0,1),
∴μ=0,σ=1.
∴P(X≤0)=0.5,
P(-2<X<2)=P(μ-2σ<X≤μ+2σ)=0.9544.
故答案为0.5,0.954 4.
点评 本题考查了正态分布的概率计算,属于基础题.

练习册系列答案
相关题目
5.从1,2,3,4,5五个数中任取3个,可组成不同的等差数列的个数为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
6.在[0,2π]上与-$\frac{π}{7}$终边相同的角是( )
| A. | $\frac{π}{7}$ | B. | $\frac{6π}{7}$ | C. | $\frac{8π}{7}$ | D. | $\frac{13π}{7}$ |
3. 如图是“向量的线性运算”知识结构图,如果要加入“三角形法则”和“平行四边形法则”,应该放在( )
如图是“向量的线性运算”知识结构图,如果要加入“三角形法则”和“平行四边形法则”,应该放在( )
 如图是“向量的线性运算”知识结构图,如果要加入“三角形法则”和“平行四边形法则”,应该放在( )
如图是“向量的线性运算”知识结构图,如果要加入“三角形法则”和“平行四边形法则”,应该放在( )| A. | “向量的加减法”中“运算法则”的下位 | |
| B. | “向量的加减法”中“运算律”的下位 | |
| C. | “向量的数乘”中“运算法则”的下位 | |
| D. | “向量的数乘”中“运算律”的下位 |
20.二次曲线$\left\{{\begin{array}{l}{x=3cosθ}\\{y=5sinθ}\end{array}}\right.$(θ是参数)的离心率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{{\sqrt{34}}}{3}$ | D. | $\frac{4}{5}$ |
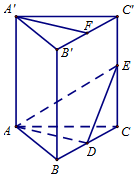 如图,在直三棱柱ABC-A'B'C'中,AB=AC,D、E分别是棱BC、CC'上的点(点D不同于点C),且AD⊥BC,F为B'C'的中点.求证:
如图,在直三棱柱ABC-A'B'C'中,AB=AC,D、E分别是棱BC、CC'上的点(点D不同于点C),且AD⊥BC,F为B'C'的中点.求证: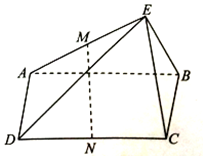 如图,在四棱锥E-ABCD中,四边形ABCD为矩形,BC⊥EB,EA⊥EB,M,N分别为AE,CD的中点,求证:
如图,在四棱锥E-ABCD中,四边形ABCD为矩形,BC⊥EB,EA⊥EB,M,N分别为AE,CD的中点,求证: