题目内容
二项式（3
+
）4的展开式的各项系数的和为p，所有二项式系数的和为q，则p：q的值为 ．
| 3 | x |
| 1 |
| x |
考点：二项式系数的性质
专题：二项式定理
分析：由题意可得，展开式的各项系数的和为p=44，所有二项式系数的和为q=24，从而求得 p：q的值．
解答：
解：令x=1可得（3
+
）4的展开式的各项系数的和为p=44，
所有二项式系数的和为q=24，∴p：q=24=16，
故答案为：16．
| 3 | x |
| 1 |
| x |
所有二项式系数的和为q=24，∴p：q=24=16，
故答案为：16．
点评：本题主要考查二项式的各项系数和、所有二项式系数的和的定义，属于中档题．
练习册系列答案
三点一测快乐周计划系列答案
相关题目
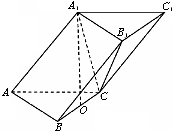在三棱柱ABC-A1B1C1中，已知AB=AC=AA1=