题目内容
如果指数函数f（x）=（a-1）x是R上的减函数，则函数g（x）=a|x|的单调递增区间为 ．
考点：指数函数的图像变换
专题：函数的性质及应用
分析：根据指数函数单调性的性质，求出a的取值范围，利用复合函数单调性之间的关系即可得到结论．
解答：
解：∵指数函数f（x）=（a-1）x是R上的减函数，
∴0＜a-1＜1，解得1＜a＜2，
设t=|x|，则根据复合函数单调性之间的性质可得，
当x≥0时，函数g（x）单调递增，
当x＜0时，函数g（x）单调递减．
故函数的递增区间是[0，+∞），
故答案为：[0，+∞）
∴0＜a-1＜1，解得1＜a＜2，
设t=|x|，则根据复合函数单调性之间的性质可得，
当x≥0时，函数g（x）单调递增，
当x＜0时，函数g（x）单调递减．
故函数的递增区间是[0，+∞），
故答案为：[0，+∞）
点评：本题主要考查复合函数单调区间的求解，根据复合函数单调性的性质是解决本题的关键．
练习册系列答案
相关题目
某程序框图如图所示，判断框内为“k≥n？”，n为正整数，若输出的S=26，则判断框内的n=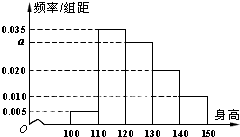
从某小学随机抽取100名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图）．由图中数据可知a=