题目内容
7.我国古代数学名著《九章算术》中,有已知长方形面积求一边的算法,其方法的前两步为:第一步:构造数列1,$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,…,$\frac{1}{n}$.①
第二步:将数列①的各项乘以n,得到数列(记为)a1,a2,a3,…,an.则a1a2+a2a3+…+an-1an=n(n-1).
分析 利用“裂项求和”方法即可得出.
解答 解:∵ak=$\frac{n}{k}$.
n≥2时,ak-1ak=$\frac{{n}^{2}}{(k-1)k}$=n2($\frac{1}{k-1}$-$\frac{1}{k}$).
∴a1a2+a2a3+…+an-1an=n2[(1-$\frac{1}{2}$)+($\frac{1}{2}$$-\frac{1}{3}$)+…+($\frac{1}{n-1}$-$\frac{1}{n}$)]=n2(1-$\frac{1}{n}$)=n(n-1).
故答案为:n(n-1)
点评 本题考查了“裂项求和”方法、数列通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.如图,网格上小正方形的边长为1,粗实线画出的是某空间几何体的三视图,则该几何体的表面积为( )
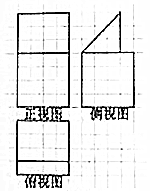

| A. | 93+12$\sqrt{2}$ | B. | 97+12$\sqrt{2}$ | C. | 105+12$\sqrt{2}$ | D. | 109+12$\sqrt{2}$ |
12.在等差数列{an}中,若a4+a6+a8+a10=80,则a1+a13的值为( )
| A. | 20 | B. | 40 | C. | 60 | D. | 80 |
16.若函数$f(x)=2sin({2x+ϕ+\frac{π}{3}})$是奇函数,且在区间$[{0,\frac{π}{4}}]$是减函数,则ϕ的值可以是( )
| A. | $-\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{π}{3}$ |
17.某三棱锥的三视图如图所示,主视图和俯视图为全等的等腰直角三角形,则该棱锥最长的棱长为( )
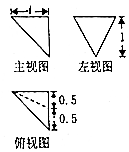

| A. | $\frac{3}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{2}$ |