题目内容
17．某三棱锥的三视图如图所示，主视图和俯视图为全等的等腰直角三角形，则该棱锥最长的棱长为（ ）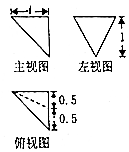
| A． | $\frac{3}{2}$ | B． | $\sqrt{3}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | $\sqrt{2}$ |
分析 由已知中的三视力可得该几何体是一个以左视图为底面的三棱锥，可得答案．
解答 解：由已知中的三视力可得该几何体是一个以左视图为底面的三棱锥，底面是底边为1，高为1的三角形，高h=1，最长的棱所在的面是直角边长分别为1，$\sqrt{1+0．{5}^{2}}$的直角三角形，斜边长为$\frac{3}{2}$，
故选：A．
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
12．某校高三年级共有学生195人，其中女生105人，男生90人．现采用按性别分层抽样的方法，从中抽取13人进行问卷调查．设其中某项问题的选择分别为“同意”、“不同意”两种，且每人都做了一种选择．下面表格中提供了被调查人答卷情况的部分信息．
（Ⅰ）完成上述统计表；
（Ⅱ）根据上表的数据估计高三年级学生该项问题选择“同意”的人数；
（Ⅲ） 从被抽取的女生中随机选取2人进行访谈，求选取的2名女生中至少有一人选择“同意”的概率．
| 同意 | 不同意 | 合计 | |
| 女学生 | 4 | 3 | 7 |
| 男学生 | 4 | 2 | 6 |
（Ⅱ）根据上表的数据估计高三年级学生该项问题选择“同意”的人数；
（Ⅲ） 从被抽取的女生中随机选取2人进行访谈，求选取的2名女生中至少有一人选择“同意”的概率．
对任意函数f（x），x∈D，可按如图所示，构造一个数列发生器，其工作原理如下：