题目内容

质点做直线运动，其速度v（t）=3t2-2t+3，则它在第2秒内所走的路程为（　　）
A、1B、3C、5D、7
考点：定积分
专题：导数的概念及应用
分析：根据积分的意义，求积分即可得到结论．
解答： 解：根据积分的意义可知，质点在第2秒内所走的路程S=
∫
2
1
(3t2-2t+3)dt=(t3-t2+3t)
|
2
1
=8-4+6-（1-1+3）=7，
故选：D．
点评：本题主要考查积分的计算，利用积分的物理意义是解决本题的关键，比较基础．
练习册系列答案
相关题目
设函数f（x）的定义域为D，如果?x∈D，?y∈D，使得f（x）=-f（y）成立，则称函数f（x）为“Ω函数”．给出下列四个函数：
①y=sinx；
②y=2x；
③y=
1
x-1
；
④f（x）=lnx，
则其中“Ω函数”共有（　　）
A、1个B、2个C、3个D、4个
已知某几何体的三视图（单位：cm）如图所示，则该几何体的表面积是（　　）
A、1cm2
B、3cm2
C、（2
3
+
15
）cm2
D、（
3
+
15
）cm2
从1，2，3，4，5，6这六个数中，每次取出两个不同的数记为a，b，则共可得到2 
b
a
的不同值的个数是（　　）
A、20B、22C、24D、28
函数f（x）的定义域为A，若x1、x2∈A且f（x1）=f（x2）时总有x1=x2，则称f（x）为单函数．例如：函数f（x）=2x+1（x∈R）是单函数．给出下列命题：
①函数f（x）=x2（x∈R）是单函数；
②指数函数f（x）=2x（x∈R）是单函数；
③若f（x）为单函数，x1、x2∈A且x1≠x2，则f（x1）≠f（x2）；
④在定义域上具有单调性的函数一定是单函数，
其中正确命题的个数是（　　）
A、3B、2C、1D、0
在星期一至星期五的5天内安排语、数、英三科测试，每天最多进行一门考试，且语文和数学不能连续两天考试，那么不同的考试安排方案种数共有（　　）
A、18B、36C、12D、48
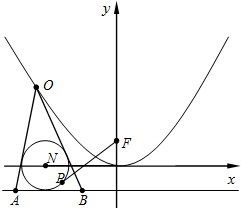已知圆N：（x+3）2+y2=1，抛物线C：y=mx2（m＞0）的焦点为（0，1）．
（Ⅰ）若P为圆N上任意一点，求|PF|的最小值及相应点P的坐标；
（Ⅱ）求证：在抛物线C上有且仅存在一个横坐标和纵坐标均为整数的点Q，使过点Q且与圆N相切的直线l1，l2，分别交抛物线的准线于点A，B，且|AB|=4
2
，并求出点Q的坐标．
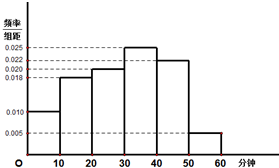电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名．如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图；将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”，已知“体育迷”中有10名女性．
（1）根据已知条件完成下面的2×2列联表．
非体育迷 体育迷 合计
男
女
合计
（2）根据列联表的独立性检验，有多大的把握认为“体育迷”与性别有关？
（3）将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”，已知“超级体育迷”中有2名女性，若从“超级体育迷”中任意选取2人，求至少有1名女性观众的概率．
参考公式：x2=
n(ad-bc)2
(a+b)(b+c)(a+c)(b+d)
（其中n=a+b+c+d）
x2≤2.706 x2＞2.706 x2＞3.841 x2＞6.635
是否有关联 没有关联 90% 95% 99%
在等差数列{an}中，已知a2=3，a5=a2+6，数列{bn}满足bn+1=2bn-1（n∈N*），且b1=3．
（Ⅰ）求通项公式an，bn；
（Ⅱ）设数列{
2
an•an+1
}的前n项和为Sn，试比较Sn与1-
1
bn
的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网