题目内容
13.已知△ABC的内角A,B,C所对的边分别为a,b,c,若(3b-c)cosA=acosC,${S_△}_{ABC}=\sqrt{2}$,则$\overrightarrow{BA}•\overrightarrow{AC}$=( )| A. | $\sqrt{2}$ | B. | 2 | C. | 1 | D. | -1 |
分析 先利用正弦定理及和角的三角函数,可求cosA的值,进而可求sinA,利用三角形的面积,求得bc.利用向量的数量积公式,即可得到结论.
解答 解:∵(3b-c)cosA=acosC,
∴由正弦定理,可得:3sinBcosA-sinCcosA=sinAcosC,
∴3sinBcosA=sinAcosC+sinCcosA,
∴3sinBcosA=sin(A+C)=sinB,
∴cosA=$\frac{1}{3}$,sinA=$\frac{2\sqrt{2}}{3}$,
∵S△ABC=$\sqrt{2}$,
∴$\frac{1}{2}$bcsinA=$\frac{\sqrt{2}}{3}$bc=$\sqrt{2}$,
∴bc=3,
∵cosA=$\frac{1}{3}$,
∴cos<$\overrightarrow{BA}$,$\overrightarrow{AC}$>=-$\frac{1}{3}$,
∴$\overrightarrow{BA}•\overrightarrow{AC}$=bccos<$\overrightarrow{BA}$,$\overrightarrow{AC}$>=-1.
故选:D.
点评 本题考查正弦定理,考查三角形的面积公式,解题的关键是利用正弦定理,进行边角互化,属于中档题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
1.下列等式一定成立的是( )
| A. | a${\;}^{-\frac{1}{2}}$•a${\;}^{\frac{1}{2}}$=0 | B. | a${\;}^{\frac{1}{2}}$÷a${\;}^{\frac{1}{3}}$=a${\;}^{\frac{5}{6}}$ | ||
| C. | (a3)2=a9 | D. | a${\;}^{\frac{1}{2}}$•a${\;}^{\frac{1}{2}}$=a |
18.下列命题中,正确的是( )
| A. | 存在x0>0,使得x0<sinx0 | |
| B. | “lna>lnb”是“10a>10b”的充要条件 | |
| C. | 若sinα≠$\frac{1}{2}$,则α≠$\frac{π}{6}$ | |
| D. | 若函数f(x)=x3+3ax2+bx+a2在x=-1有极值0,则a=2,b=9或a=1,b=3 |
2.已知全集U={1,2,3,4,5,6},A={1,2,5},B={2,3,4},则A∩(∁UB)=( )
| A. | {2,6} | B. | {1,5} | C. | {1,6} | D. | {5,6} |
3.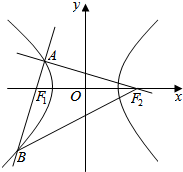 如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若($\overrightarrow{AB}$+$\overrightarrow{A{F}_{2}}$)•$\overrightarrow{B{F}_{2}}$=0,则双曲线的离心率为( )
如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若($\overrightarrow{AB}$+$\overrightarrow{A{F}_{2}}$)•$\overrightarrow{B{F}_{2}}$=0,则双曲线的离心率为( )
 如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若($\overrightarrow{AB}$+$\overrightarrow{A{F}_{2}}$)•$\overrightarrow{B{F}_{2}}$=0,则双曲线的离心率为( )
如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若($\overrightarrow{AB}$+$\overrightarrow{A{F}_{2}}$)•$\overrightarrow{B{F}_{2}}$=0,则双曲线的离心率为( )| A. | $\sqrt{5+2\sqrt{2}}$ | B. | $\sqrt{5-2\sqrt{2}}$ | C. | $\sqrt{4+2\sqrt{2}}$ | D. | $\sqrt{4-2\sqrt{2}}$ |
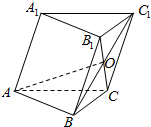 已知斜三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,∠BAA1=$\frac{2π}{3}$,∠CAA1=$\frac{π}{3}$,AB=AC=1,AA1=2,点O是B1C与BC1的交点.
已知斜三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,∠BAA1=$\frac{2π}{3}$,∠CAA1=$\frac{π}{3}$,AB=AC=1,AA1=2,点O是B1C与BC1的交点.