题目内容
已知集合A={x|2a≤x<a+3},B={x|2x<
或log5x>1}.
(1)若a=-1,求A∪B;(∁RA)∩B;
(2)若A∩B=∅,求a的取值范围.
| 1 |
| 2 |
(1)若a=-1,求A∪B;(∁RA)∩B;
(2)若A∩B=∅,求a的取值范围.
考点:交集及其运算,交、并、补集的混合运算
专题:集合
分析:(1)若a=-1,化简集合,即可求A∪B;(∁RA)∩B;
(2)根据A∩B=∅,建立条件关系即可.
(2)根据A∩B=∅,建立条件关系即可.
解答:
解:(1)当a=-1时,A={x|-2≤x<2},B={x|2x<
或log5x>1}={x|x<-1或x>5}.
则A∪B={x|x>5或x<2};(∁RA)∩B={x|x>5或x<-2}.
(2)当A=∅时,2a≥a+3,解得a≥3
当A≠∅,若A∩B=∅,则
,解得-
≤a≤2
综上所述,a的取值范围{a|a≥3或-
≤a≤2}.
| 1 |
| 2 |
则A∪B={x|x>5或x<2};(∁RA)∩B={x|x>5或x<-2}.
(2)当A=∅时,2a≥a+3,解得a≥3
当A≠∅,若A∩B=∅,则
|
| 1 |
| 2 |
综上所述,a的取值范围{a|a≥3或-
| 1 |
| 2 |
点评:本题主要考查集合的基本运算以及集合关系的应用,注意要对集合进行讨论.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
sinα=
,α∈(
,π),则cos(
-α)=( )
| 3 |
| 5 |
| π |
| 2 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设集合A={x|x=2k-1,k∈Z},则( )
| A、3∈A | B、3∉A |
| C、3⊆A | D、3?A |
命题“若x>2,则x>0”的否命题是( )
| A、若x>2,则x≤0 |
| B、若x≤2,则x>0 |
| C、若x≤2,则x≤0 |
| D、若x<2,则x<0 |
函数f(x)=
的定义域为( )
| 1 |
| log3(3x-2) |
A、[
| ||
B、(
| ||
C、[
| ||
D、(
|
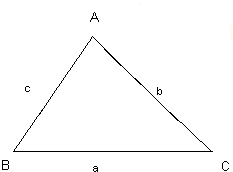 已知锐角△ABC,满足(2a-c)cosB=bcosc,
已知锐角△ABC,满足(2a-c)cosB=bcosc,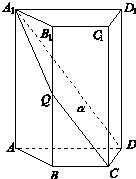 如图,四棱柱ABCD A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC.过A1,C,D三点的平面记为α,BB1与α的交点为Q.
如图,四棱柱ABCD A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC.过A1,C,D三点的平面记为α,BB1与α的交点为Q.