题目内容
设集合A={x|x2+（b+2）x+b+1=0}，则A中所有元素的和S= ．
考点：函数的零点
专题：函数的性质及应用
分析：解方程求出A中的元素，求和即可．
解答：
解：∵x2+（b+2）x+b+1=0，
∴（x+b+1）（x+1）=0，
∴x=-b-1，x=-1，
∴A={-b-1，-1}，
∴S=-（b+2），
故答案为：-b-2．
∴（x+b+1）（x+1）=0，
∴x=-b-1，x=-1，
∴A={-b-1，-1}，
∴S=-（b+2），
故答案为：-b-2．
点评：本题考查了函数的零点问题，考查一元二次方程的解法，是一道基础题．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
一元二次方程2x2-6x-3=0的两根为x1，x2，则（1+x1）（1+x2）的值为（ ）
| A、3 | ||
| B、6 | ||
| C、-3 | ||
D、
|
已知集合A={0，1，2，3}，B={1，3，4}，则A∩B的子集个数为（ ）
| A、2 | B、3 | C、4 | D、16 |
在△ABC中，内角A，B，C的对边分别是a，b，c，若a2-b2-c2=
bc，A=（ ）
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
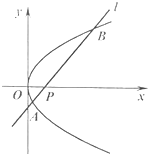如图，已知抛物线y2=4x，点P（a，0）是x轴上的一点，经过点P且斜率为1的直线l与抛物线相交于A，B两点．