Question

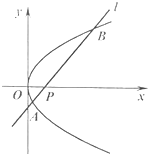如图，已知抛物线y²=4x，点P（a，0）是x轴上的一点，经过点P且斜率为1的直线l与抛物线相交于A，B两点．
（1）当点P在x轴上时，求线段AB的中点轨迹方程；
（2）若|AB|=4|OP|（O为坐标原点），求a的值．

Answer 1

考点：抛物线的简单性质

专题：圆锥曲线的定义、性质与方程

分析：（1）设A（x₁，y₁），B（x₂，y₂），AB中点为M（x₀，y₀）．利用中点坐标公式、斜率计算公式、“点差法”即可得出．
（2）把直线l：x=y+a的方程与抛物线的方程联立可得根与系数的关系，利用弦长公式、两点之间的距离公式即可得出．

解答： 解：（1）设A（x₁，y₁），B（x₂，y₂），AB中点为M（x₀，y₀）．
则

y 2 1 =4x1 y 2 2 =4x2

，化为（y₁+y₂）（y₁-y₂）=4（x₁-x₂），
又

y1-y2

x1-x2

=1，y₁+y₂=2y₀，
∴2y₀=4，从而y₀=2．
故线段AB的中点轨迹的方程是：y=2（x＞1）．
（2）直线l：x=y+a，
由

x=y+a y2=4x

，化为y²-4y-4a=0．
△=16+16a＞0，解得a＞-1．
∴y₁+y₂=4，y₁y₂=-4a．
|AB|=

2

|y1-y2|
=

2

(y1+y2)2-4y1y2

=

2

16+16a

=4

2(1+a)

．
若|AB|=4|OP|，则4

2(1+a)

=4|a|，即a²-2a-2=0．
解得：a=1±

3

．

点评：本题考查了抛物线的标准方程及其性质、中点坐标公式、斜率计算公式、“点差法”、弦长公式，考查了推理能力与计算能力，属于难题．