题目内容
已知递减等差数列{an}中,a3a7=-16,a4+a6=0.
(1)求数列通项公式an
(2)求数列{|an|}前n项和Sn.
(1)求数列通项公式an
(2)求数列{|an|}前n项和Sn.
考点:数列的求和,等差数列的通项公式
专题:等差数列与等比数列
分析:本题(1)先利用等差数列的通项公式列出方程组,求出数列的首项和公差,得到数列的通项公式;(2)分类讨论后,利用等差数列和前n项公式求前n项和,得到本题结论.
解答:
解:(1)设{an}的公差为d,则
,
即
,
解得
或
,
∵an为递减数列,
∴an=10-2n.
(2)当n≤5,an≥0,n≥6,an<0,
当n≤5时,Sn=8+6+…+(10-2n)=
×n=9n-n2;
;
;
当n>5时,Sn=a1+a2+…+a5-(a6+a7+…+an)
=2(a1+a2+…+a5)-(a1+a2+…+an)
=40-(9n-n2)
=n2-9n+40.
.
|
即
|
解得
|
|
∵an为递减数列,
∴an=10-2n.
(2)当n≤5,an≥0,n≥6,an<0,
当n≤5时,Sn=8+6+…+(10-2n)=
| 8+(10-2n) |
| 2 |
;
;
当n>5时,Sn=a1+a2+…+a5-(a6+a7+…+an)
=2(a1+a2+…+a5)-(a1+a2+…+an)
=40-(9n-n2)
=n2-9n+40.
|
点评:本题考查了等差数列的通项公式和前n项公式的应用,还考查了分类讨论思想和转化化归思想,有一定的思维量,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在正方体ABCD-A1B1C1D1中,E是C1D1的中点,正方体棱长为2,求异面直线DE与AC所成角的余弦值.
如图,在正方体ABCD-A1B1C1D1中,E是C1D1的中点,正方体棱长为2,求异面直线DE与AC所成角的余弦值.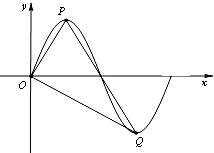 某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<
某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<