题目内容
已知函数f(x)=
(1)作出函数f(x)的图象,并求函数f(x)的单调区间;
(2)求集合M={m|使方程f(x)=m有三个不相等的实数根}.
|
(1)作出函数f(x)的图象,并求函数f(x)的单调区间;
(2)求集合M={m|使方程f(x)=m有三个不相等的实数根}.
考点:函数图象的作法,函数的零点与方程根的关系
专题:函数的性质及应用
分析:(1)由已知中函数f(x)的解析式,根据分段函数图象分段画的原则,结合二次函数的图象和性质,可得函数f(x)的图象,进而根据图象上升和下降情况,找到函数f(x)的单调区间;
(2)由(1)中图象可得0<m<f(
)时,方程f(x)=m有三个不相等的实数根,进而得到满足条件的集合M.
(2)由(1)中图象可得0<m<f(
| 3 |
| 2 |
解答:
解:(1)函数f(x)=
的图象如下图所示:
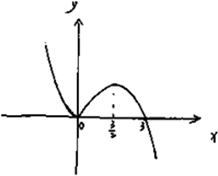
由图可知,函数f(x)的单调增区间为:(0,
),
函数f(x)的单调减区间为:(-∞,0),(
,+∞)…(6分)
(2)由图可知,0<m<f(
)时,方程f(x)=m有三个不相等的实数根,
又f(
)=-(
)2+3×
=
,
∴0<m<
∴M={m|0<m<
}…(12分)
|

由图可知,函数f(x)的单调增区间为:(0,
| 3 |
| 2 |
函数f(x)的单调减区间为:(-∞,0),(
| 3 |
| 2 |
(2)由图可知,0<m<f(
| 3 |
| 2 |
又f(
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
∴0<m<
| 9 |
| 4 |
∴M={m|0<m<
| 9 |
| 4 |
点评:本题考查的知识点是函数图象的作法,函数的零点与方程根的关系,数形结合是解答的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目