题目内容
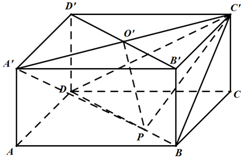 如图,在长方体ABCD-A′B′C′D′中,DA=DC=2,DD′=1,A′C′与B′D′相交于点O′,点P在线段BD上(点P与点B不重合).
如图,在长方体ABCD-A′B′C′D′中,DA=DC=2,DD′=1,A′C′与B′D′相交于点O′,点P在线段BD上(点P与点B不重合).(1)若异面直线O′P与BC′所成角的余弦值为
| ||
| 55 |
(2)若DP=
3
| ||
| 2 |
考点:二面角的平面角及求法,异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:(1)以
,
,
为一组正交基底,建立空间直角坐标系D-xyz,由此利用向量法能求出DP的长度.(2)求出平面DC'B的法向量和平面PA'C'的法向量,利用向量法求出设平面PA'C'与平面DC'B所成角的余弦值,由此能求出平面PA′C′与平面DC′B所成角的正弦值.
| DA |
| DC |
| DD′ |
解答:
 解:(1)以
解:(1)以
,
,
为一组正交基底,
建立如图所示的空间直角坐标系D-xyz,
由题意,知D(0,0,0),A'(2,0,1),B(2,2,0),C'(0,2,1),O'(1,1,1).设P(t,t,0),
∴
=(t-1,t-1,-1),
=(-2,0,1).
设异面直线O'P与BC'所成角为θ,
则cosθ=
=
=
,
化简得:21t2-20t+4=0,
解得:t=
或t=
,DP=
或DP=
.…(5分)
(2)∵DP=
,∴P(
,
,0),
=(0,2,1),
=(2,2,0),
=(
,-
,1),
=(-
,
,1),
设平面DC'B的一个法向量为
=(x1,y1,z1),
∴
,∴
,
即
,取y1=-1,
=(1,-1,2),
设平面PA'C'的一个法向量为
=(x2,y2,z2),
∴
,∴
,
即
,取y2=1,
=(1,1,1),
设平面PA'C'与平面DC'B所成角为φ,
∴|cosφ|=
=
=
,
∴sinφ=
.…(10分)
 解:(1)以
解:(1)以| DA |
| DC |
| DD′ |
建立如图所示的空间直角坐标系D-xyz,
由题意,知D(0,0,0),A'(2,0,1),B(2,2,0),C'(0,2,1),O'(1,1,1).设P(t,t,0),
∴
| O′P |
| BC′ |
设异面直线O'P与BC'所成角为θ,
则cosθ=
|
| ||||
|
|
| |-2(t-1)-1| | ||||
|
| ||
| 55 |
化简得:21t2-20t+4=0,
解得:t=
| 2 |
| 3 |
| 2 |
| 7 |
| 2 |
| 3 |
| 2 |
| 2 |
| 7 |
| 2 |
(2)∵DP=
3
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| DC′ |
| DB |
| PA′ |
| 1 |
| 2 |
| 3 |
| 2 |
| PC′ |
| 3 |
| 2 |
| 1 |
| 2 |
设平面DC'B的一个法向量为
| n1 |
∴
|
|
即
|
| n1 |
设平面PA'C'的一个法向量为
| n2 |
∴
|
|
即
|
| n2 |
设平面PA'C'与平面DC'B所成角为φ,
∴|cosφ|=
|
| ||||
|
|
| 2 | ||||
|
| ||
| 3 |
∴sinφ=
| ||
| 3 |
点评:本题考查线段长的求法,考查二面角的正弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
下列各函数中,其图象经过点(1,0)的是( )
| A、y=x2+1 | ||
B、y=
| ||
| C、y=3x | ||
| D、y=log2x |
把半径是3,4,5的三个铁球熔铸成一个大球,则大球的体积是( )
| A、298π | B、288π |
| C、144π | D、72π |
已知命题p:?x0∈R,x0n+a1x0n-1+a2x0n-2+…+an≤0,则( )
| A、¬p:?x∈R,xn+a1xn-1+a2xn-2+…+an≤0 |
| B、¬p:?x0∈R,x0n+a1x0n-1+a2x0n-2+…+an>0 |
| C、¬p:?x∈R,xn+a1xn-1+a2xn-2+…+an>0 |
| D、¬p:?x0∈R,x0n+a1x0n-1+a2x0n-2+…+an≥0 |
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,AD=1,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,AD=1,PD⊥底面ABCD.