题目内容
(1)求函数y=
的定义域;
(2)已知f(x)=
,求f(
)+f(
)的值.
log2
|
(2)已知f(x)=
|
| 1 |
| 3 |
| 4 |
| 3 |
考点:函数的定义域及其求法,函数的值
专题:函数的性质及应用
分析:(1)根据函数成立的条件即可求出函数的定义域;
(2)利用分段函数直接代入即可得到结论.
(2)利用分段函数直接代入即可得到结论.
解答:
解:(1)要使函数y=
有意义,则log2
-1≥0,即
≥2,0<sinx≤
,即2kπ<x≤2kπ+
或2kπ+
≤x<2kπ+π,
即函数的定义域为{x|2kπ<x≤2kπ+
或2kπ+
≤x<2kπ+π,k∈Z}.
(2)f(
)=cos
=
,f(
)=f(
)-1=
-1=-
,
则f(
)+f(
)=
-
=0.
log2
|
| 1 |
| sinx |
| 1 |
| sinx |
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
即函数的定义域为{x|2kπ<x≤2kπ+
| π |
| 6 |
| 5π |
| 6 |
(2)f(
| 1 |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
则f(
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查函数定义域的求法以及函数值的计算,要求熟练掌握常见函数成立的条件.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
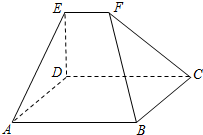 如图,在五面体ABCDEF中,四边形ABCD是矩形,DE⊥平面ABCD.
如图,在五面体ABCDEF中,四边形ABCD是矩形,DE⊥平面ABCD.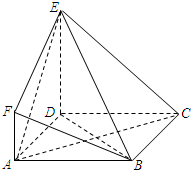 如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,BE与平面ABCD所成角的正切值为
如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,BE与平面ABCD所成角的正切值为