题目内容
设函数f(x)=
(x>0),数列{an}满足a1=1,an=f(
)(x∈N*,且n≥2).
(1)求数列{an}的通项公式;
(2)设Tn=a1a2-a2a3+a3a4-a4a5+…+(-1)n-1anan+1,若Tn≥tn2对n∈N*恒成立,求实数t的取值范围;
(3)是否存在以a1为首项,公比为q(0<q<5,q∈N*)的等比数列{a nk},k∈N*,使得数列{a nk}中每一项都是数列{an}中不同的项,若存在,求出所有满足条件的数列{nk}的通项公式;若不存在,说明理由.
| 2x+1 |
| x |
| 1 |
| an-1 |
(1)求数列{an}的通项公式;
(2)设Tn=a1a2-a2a3+a3a4-a4a5+…+(-1)n-1anan+1,若Tn≥tn2对n∈N*恒成立,求实数t的取值范围;
(3)是否存在以a1为首项,公比为q(0<q<5,q∈N*)的等比数列{a nk},k∈N*,使得数列{a nk}中每一项都是数列{an}中不同的项,若存在,求出所有满足条件的数列{nk}的通项公式;若不存在,说明理由.
考点:数列与函数的综合
专题:综合题,等差数列与等比数列
分析:(1)由an=f(
),f(x)=
(x∈N*,且n≥2),知an-an-1=2.再由a1=1,能求出数列{an}的通项公式;
(2)当n=2m,m∈N*时,Tn=-2n(n+1);当n=2m-1,m∈N*时,Tn=2n2+6n+3,由此入手能求出实数t的取值范围.
(3)由an=2n-1,知数列{an}中每一项都是奇数.当q=1时,显然不存在这样的数列{ank}.当q=3时,an1=1,n1=1,所以ank=3k-1=2nk-1,可得满足条件的数列{nk}的通项公式.
| 1 |
| an-1 |
| 2x+1 |
| x |
(2)当n=2m,m∈N*时,Tn=-2n(n+1);当n=2m-1,m∈N*时,Tn=2n2+6n+3,由此入手能求出实数t的取值范围.
(3)由an=2n-1,知数列{an}中每一项都是奇数.当q=1时,显然不存在这样的数列{ank}.当q=3时,an1=1,n1=1,所以ank=3k-1=2nk-1,可得满足条件的数列{nk}的通项公式.
解答:
解:(1)因为an=f(
),f(x)=
(x∈N*,且n≥2),
所以an-an-1=2.
因为a1=1,
所以数列{an}是以1为首项,公差为2的等差数列.
所以an=2n-1;
(2)①当n=2m,m∈N*时,Tn=T2m=a1a2-a2a3+a3a4-a4a5+…+(-1)2m-1a2ma2m+1=a2(a1-a3)+a4(a3-a5)+…+a2m(a2m-1-a2m+1)=-4(a2+a4+…+a2m)=-4(2m+1)m=-2n(n+1);
②当n=2m-1,m∈N*时,Tn=T2m-1=T2m-(-1)2m-1a2ma2m+1=2n2+6n+3
要使Tn≥tn2对n∈N*恒成立,
只要使-2n(n+1)≥tn2,(n为偶数)恒成立.
只要使-2(1+
)≥t,对n为偶数恒成立,
故实数t的取值范围为(-∞,3];
(3)由an=2n-1,知数列{an}中每一项都是奇数.
当q=1时,显然不存在这样的数列{ank}.
当q=3时,若存在以a1为首项,公比为3的数列{ank},k∈N*.
则an1=1,n1=1,所以ank=3k-1=2nk-1,
所以nk=
.
所以满足条件的数列{nk}的通项公式为nk=
.
| 1 |
| an-1 |
| 2x+1 |
| x |
所以an-an-1=2.
因为a1=1,
所以数列{an}是以1为首项,公差为2的等差数列.
所以an=2n-1;
(2)①当n=2m,m∈N*时,Tn=T2m=a1a2-a2a3+a3a4-a4a5+…+(-1)2m-1a2ma2m+1=a2(a1-a3)+a4(a3-a5)+…+a2m(a2m-1-a2m+1)=-4(a2+a4+…+a2m)=-4(2m+1)m=-2n(n+1);
②当n=2m-1,m∈N*时,Tn=T2m-1=T2m-(-1)2m-1a2ma2m+1=2n2+6n+3
要使Tn≥tn2对n∈N*恒成立,
只要使-2n(n+1)≥tn2,(n为偶数)恒成立.
只要使-2(1+
| 1 |
| n |
故实数t的取值范围为(-∞,3];
(3)由an=2n-1,知数列{an}中每一项都是奇数.
当q=1时,显然不存在这样的数列{ank}.
当q=3时,若存在以a1为首项,公比为3的数列{ank},k∈N*.
则an1=1,n1=1,所以ank=3k-1=2nk-1,
所以nk=
| 3k-1+1 |
| 2 |
所以满足条件的数列{nk}的通项公式为nk=
| 3k-1+1 |
| 2 |
点评:本题考查数列与函数的综合,考查数列的通项与求和,考查恒成立问题,考查学生分析解决问题的能力,有难度.

练习册系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.若sinC+sin(B-A)=sin2A,则△ABC的形状为( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰三角形或直角三角形 |
 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=2
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=2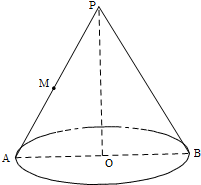 已知圆锥母线长为6,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,底面半径OC与母线PB所成的角的大小等于θ.
已知圆锥母线长为6,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,底面半径OC与母线PB所成的角的大小等于θ.