题目内容
设△AOB的顶点均在抛物线y2=2px(p>O)上,其中O为坐标原点,若△AOB的垂心恰好是抛物线的焦点,求△AOB的面积.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:如图所示,由于△AOB的垂心恰好是抛物线的焦点F(
,0),可得AB⊥x轴.设A(s,t),B(s,-t),t2=2ps(s>0).利用
•
=0即可解出三s,t.
| p |
| 2 |
| AF |
| OB |
解答:
解:如图所示,∵△AOB的垂心恰好是抛物线的焦点F(
,0),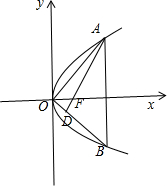
∴AB⊥x轴.
设A(s,t),B(s,-t),t2=2ps(s>0).
∵AF⊥OB,
∴
•
=(
-s,-t)•(s,-t)=s(
-s)+t2=0,
把t2=2ps代入上式可得:s(
-s)+2ps=0.
化为s=
,∴t2=5p2.
∴△AOB的面积S=
×
×2
p=
.
| p |
| 2 |

∴AB⊥x轴.
设A(s,t),B(s,-t),t2=2ps(s>0).
∵AF⊥OB,
∴
| AF |
| OB |
| p |
| 2 |
| p |
| 2 |
把t2=2ps代入上式可得:s(
| p |
| 2 |
化为s=
| 5p |
| 2 |
∴△AOB的面积S=
| 1 |
| 2 |
| 5p |
| 2 |
| 5 |
5
| ||
| 2 |
点评:本题考查了抛物线的标准方程及其性质、向量垂直与数量积的关系、三角形的垂心的性质,考查了推理能力与与计算能力,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知数列{an}是等差数列,且a3+a4+a5+a6+a7=160,则a1+a9=( )
| A、32 | B、64 | C、96 | D、128 |
给出下列四个命题:其中真命题的是( )
| A、命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” |
| B、命题“?x∈R,x2+x-1<0”的否定是“?x∈R,x2+x-1>0” |
| C、命题“若x=y,则sinx=siny”的逆否命题为真命题 |
| D、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
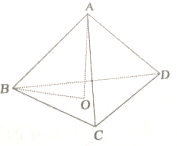 如图,四面体ABCD中,AB、AC、AD两两垂直,若△BCD的垂心为O,求证:AO⊥平面BCD.
如图,四面体ABCD中,AB、AC、AD两两垂直,若△BCD的垂心为O,求证:AO⊥平面BCD.