已知数列{an}的前n项和公式为Sn=n2-6n+3.则a7+a8+a9+a10等于( ) A.7B.13C.33D.40 题目和参考答案——青夏教育精英家教网—

题目内容

已知数列{a_n}的前n项和公式为S_n=n²-6n+3，则a₇+a₈+a₉+a₁₀等于（　　）

A、7

B、13

C、33

D、40

考点：数列的求和

专题：等差数列与等比数列

分析：由已知条件利用a₇+a₈+a₉+a₁₀=S10 -S₆，能求出结果．

解答： 解：∵数列{a_n}的前n项和公式为S_n=n²-6n+3，
∴a₇+a₈+a₉+a₁₀
=S10 -S₆
=（10²-6×10+3）-（6²-6×6+3）
=40．
故选：D．

点评：本题考查数列的前n项和公式的应用，是基础题，解题时要认真审题，熟练掌握数列前n项和的性质．

练习册系列答案

金榜一号同步单元全程达标测试AB卷系列答案

下列命题中，正确的个数是（　　）
①若直线l上有无数个点不在平面α内，则l∥α；
②若直线l∥平面α，则直线l与平面α 内任意一条直线都平行；
③如果两条平行直线中的一条与一个平面平行，那么另一条也与这个平面平行；
④若直线l∥平面α，则直线l与平面α 内的任意一条直线都没有公共点；
⑤若两条直线都与第三条直线垂直，则这两条直线互相平行．

已知函数fn(x)=anx3+bnx2+cnx，满足

an+1

bn+1

cn+1

=q(q＞1，q为常数)，n∈N^*，给出下列说法：①函数f_n（x）为奇函数；
②若函数f₁（x）在R上单调递增，则a₁＞0；
③若x₀是函数f_n（x）的极值点，则x₀也是函数f_n+1（x）的极值点；
④若bn2＞3ancn，则函数f_n（x）在R上有极值．
以上说法正确的个数是（　　）

设△ABC中，边a，b，c的对角分别为A，B，C，且acosC+

c=b．
（1）求A的大小；
（2）若a=1，求△ABC面积S的取值范围．

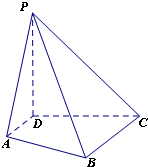在四棱锥P-ABCD中，PD⊥平面ABCD，PD=CD=BC=2AD，AD∥BC，∠BCD=90°．
（Ⅰ）求证：BC⊥PC；
（Ⅱ）求PA与平面PBC所成角的正弦值；
（Ⅲ）线段PB上是否存在点E，使AE⊥平面PBC？说明理由．

已知p：x²-2x-3≤0，q：1-m≤x≤1+m（m＞0）．
（Ⅰ）当m=1时，p∧q为真命题，求x的取值范围；
（Ⅱ）若p是q的充分条件，求实数m的取值范围．

试题分类