题目内容
10.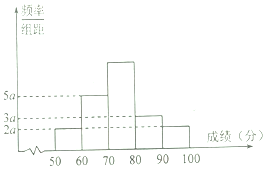 某学习小组20名学生一次数学考试成绩(单位:分)频率直方图如图所示,已知前三个矩形框垂直于横轴的高度成等差数列.
某学习小组20名学生一次数学考试成绩(单位:分)频率直方图如图所示,已知前三个矩形框垂直于横轴的高度成等差数列.(1)求频率分布直方图中a的值;
(2)分别求出成绩落在[50,60)与[80,90)中的学生人数;
(3)从成绩在[50,60)与[80,90)中的学生中人选2人,求此2人的成绩相差20分以上的概率.
分析 (1)由已知前三个长方形的高成等差数列知,第三个长方形的高为8a,再由频率分布直方图能求出a.
(2)由频率分布直方图,能求出成绩落在[50,60)与[80,90)中的学生人数.
(3)记成绩落在 中的2人为A1,A2,成绩落在 中的3人为B1,B2,B3,利用列举法能求出这2人的成绩相差20分以上的概率.
解答 解:(1)由已知前三个长方形的高成等差数列知,第三个长方形的高为8a,
于是由频率分布直方图得(2a+5a+8a+3a+2a)×10=1,解得a═0.005.…(2分)
(2)由频率分布直方图,知:
成绩落在[50,60)中的学生人数为2×0.005×10×20=2,
成绩落在[80,90)中的学生人数为3×0.005×10×20=3.…(4分)
(3)记成绩落在 中的2人为A1,A2,成绩落在 中的3人为B1,B2,B3,
则从成绩在 与 中任选2人的基本事件共有10个:
(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A2,B1),
(A2,B2),(A2,B3),(B1,B2),(B1,B3),(B2,B3),…(7分)
其中2人的成绩相差20分以上的基本事件有6个:
(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),
故这2人的成绩相差20分以上的概率P=$\frac{6}{10}=\frac{3}{5}$.…(10分)
点评 本题考查等差数列、频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
1.在△ABC中,a、b、c分别为角A、B、C所对的边,且a=2,b=$\sqrt{6}$,B=$\frac{π}{3}$,则角A等于( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$或$\frac{3π}{4}$ |
5.若关于x的方程$\sqrt{-{x}^{2}+4x-3}$=mx+m-1有两个不同的实数根,则实数m的取值范围是( )
| A. | (0,$\frac{3}{4}$) | B. | [$\frac{1}{2}$,$\frac{3}{4}$) | C. | ($\frac{1}{4}$,$\frac{1}{2}$) | D. | [$\frac{1}{4}$,$\frac{3}{4}$) |
15.在等差数列{an}中,a4+a6=6,且a2=1,则公差d等于( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{3}{5}$ |