题目内容
为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95),由此得到频率分布直方图,如右图.
估算众数,中位数,平均数.
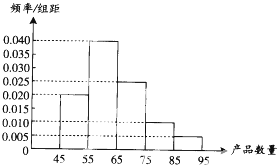
估算众数,中位数,平均数.

考点:频率分布直方图
专题:概率与统计
分析:根据频率分布直方图提供的信息,在频率分布直方图中,众数是最高的小长方形的底边的中点横坐标的值,中位数是所有小长方形的面积相等的分界线,平均数是各小长方形底边中点的横坐标与对应频率的积的和,由此求出即可.
解答:
解:由频率分布直方图可知,众数为
=60;
因为0.2+0.4>0.5,所以中位数一定在[55,65]之间,设中位数为x,则0.2+(x-55)×0.04=0.5,解得x=62.5,
所以中位数为62.5,
平均数为(50×0.02+60×0.04+70×0.025+80×0.01+90×0.005)×10=64,所以平均数64;
| 55+65 |
| 2 |
因为0.2+0.4>0.5,所以中位数一定在[55,65]之间,设中位数为x,则0.2+(x-55)×0.04=0.5,解得x=62.5,
所以中位数为62.5,
平均数为(50×0.02+60×0.04+70×0.025+80×0.01+90×0.005)×10=64,所以平均数64;
点评:本题考查了频率分布直方图岁反映的调查数据;在频率分布直方图中,根据众数、中位数和平均数的意义,众数是最高的小长方形的底边的中点横坐标的值,中位数是所有小长方形的面积相等的分界线,平均数是各小长方形底边中点的横坐标与对应频率的积的和.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
已知集合A={x|x2-2x<0},B={x|-
<x<
},则( )
| 5 |
| 5 |
| A、A∩B=∅ | B、A∪B=R |
| C、B⊆A | D、A⊆B |
设a>b>0,则下列不等式成立的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,某几何体的下部分是长为8,宽为6,高为3的长方体,上部分是侧棱长都相等且高为3的四棱锥,求:
如图,某几何体的下部分是长为8,宽为6,高为3的长方体,上部分是侧棱长都相等且高为3的四棱锥,求: