题目内容
已知两个非零向量
，
满足（
+
）⊥（2
-
），（
-2
）⊥（2
+
），求向量
，
夹角的余弦值．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：设向量
，
的夹角为θ，由垂直可得2
2+
•
-
2=0和2
2-3
•
-2
2=0，两式联立可解．
| a |
| b |
| a |
| a |
| b |
| b |
| a |
| a |
| b |
| b |
解答：
解：设向量
，
的夹角为θ，
∵（
+
）⊥（2
-
），（
-2
）⊥（2
+
），
∴（
+
）•（2
-
）=0，（
-2
）•（2
+
）=0，
∴2
2+
•
-
2=0，①2
2-3
•
-2
2=0，②，
①×3+②可得8
2=5
2，∴
2=
2，∴|
|=
|
|，
代入①可得
|
|2+
|
||
|cosθ-|
|2=0，
解得cosθ=-
，
∴向量
，
夹角的余弦值为-
| a |
| b |
∵（
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
∴（
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
∴2
| a |
| a |
| b |
| b |
| a |
| a |
| b |
| b |
①×3+②可得8
| a |
| b |
| a |
| 5 |
| 8 |
| b |
| a |
| ||
| 4 |
| b |
代入①可得
| 5 |
| 4 |
| b |
| ||
| 4 |
| b |
| b |
| b |
解得cosθ=-
| ||
| 10 |
∴向量
| a |
| b |
| ||
| 10 |
点评：本题考查数量积与向量的夹角，属基础题．
练习册系列答案
相关题目
将函数y=sin（2x+
）的图象沿x轴向左平移m（m＞0）个单位后，得到一个奇函数的图象，则m的最小值为（ ）
| π |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若球的半径扩大到原来的2倍，那么体积扩大到原来的（ ）
| A、64倍 | B、16倍 |
| C、8倍 | D、4倍 |
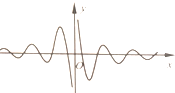函数y=f（x）的图象如图所示，则f（x）可能是（ ）| A、xsinx | ||
| B、xcosx | ||
C、
| ||
D、
|