题目内容
点 A,B,C,D在同一球面上,AB=BC=
,AC=2,若球的表面积为
,则四面体ABCD体积的最大值为 .
| 2 |
| 25π |
| 4 |
考点:球的体积和表面积,棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:根据几何体的特征,判定外接球的球心,求出球的半径,即可求出球的表面积.
解答:
 解:根据题意知,△ABC是一个直角三角形,其面积为1.其所在球的小圆的圆心在斜边AC的中点上,设小圆的圆心为Q,球的半径为r,
解:根据题意知,△ABC是一个直角三角形,其面积为1.其所在球的小圆的圆心在斜边AC的中点上,设小圆的圆心为Q,球的半径为r,
因为球的表面积为
,
所以4πr2=
所以r=
,
四面体ABCD的体积的最大值,底面积S△ABC不变,高最大时体积最大,
就是D到底面ABC距离最大值时,h=r+
=2.
四面体ABCD体积的最大值为
×S△ABC×h=
×
×
×
×2=
,
故答案为:
.
 解:根据题意知,△ABC是一个直角三角形,其面积为1.其所在球的小圆的圆心在斜边AC的中点上,设小圆的圆心为Q,球的半径为r,
解:根据题意知,△ABC是一个直角三角形,其面积为1.其所在球的小圆的圆心在斜边AC的中点上,设小圆的圆心为Q,球的半径为r,因为球的表面积为
| 25π |
| 4 |
所以4πr2=
| 25π |
| 4 |
所以r=
| 5 |
| 4 |
四面体ABCD的体积的最大值,底面积S△ABC不变,高最大时体积最大,
就是D到底面ABC距离最大值时,h=r+
| r2-12 |
四面体ABCD体积的最大值为
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题考查的知识点是球内接多面体,球的表面积,其中分析出何时四面体ABCD的体积的最大值,是解答的关键.

练习册系列答案
相关题目
函数y=
的定义域为( )
log
|
A、(1,
| ||
B、[1,
| ||
| C、(1,2] | ||
| D、(1,2) |
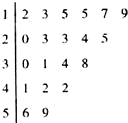 为了解某校教师使用多媒体辅助教学的情况,采用简单随机抽样的方法,从该校200名授课教师中抽取20名教师,调查了解他们上学期使用多媒体辅助教学的次数,结果用茎叶图表示(如图),据此可估计该校上学期200名教师中,使用多媒体辅助教学不少于30次的教师人数为
为了解某校教师使用多媒体辅助教学的情况,采用简单随机抽样的方法,从该校200名授课教师中抽取20名教师,调查了解他们上学期使用多媒体辅助教学的次数,结果用茎叶图表示(如图),据此可估计该校上学期200名教师中,使用多媒体辅助教学不少于30次的教师人数为