题目内容
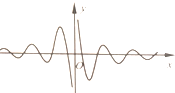函数y=f（x）的图象如图所示，则f（x）可能是（ ）| A、xsinx | ||
| B、xcosx | ||
C、
| ||
D、
|
考点：余弦函数的奇偶性,奇偶函数图象的对称性,函数的图象
专题：函数的性质及应用
分析：根据函数的图象确定函数的定义域，奇偶性和单调性进行判断即可．
解答：
解：由图象知函数的定义域为{x|x≠0}，故排除A，B，
函数的图象关于原点对称，即函数为奇函数，
∵f（x）=
是偶函数，不满足条件，
∴f（x）=
是奇函数，满足条件，
故选D
函数的图象关于原点对称，即函数为奇函数，
∵f（x）=
| sinx |
| x |
∴f（x）=
| cosx |
| x |
故选D
点评：本题主要考查函数图象的识别和判断，根据函数的图象，确定函数的定义域，奇偶性和对称性是解决本题的关键．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
相关题目
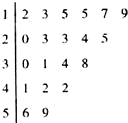为了解某校教师使用多媒体辅助教学的情况，采用简单随机抽样的方法，从该校200名授课教师中抽取20名教师，调查了解他们上学期使用多媒体辅助教学的次数，结果用茎叶图表示（如图），据此可估计该校上学期200名教师中，使用多媒体辅助教学不少于30次的教师人数为函数f（x）=2x+3x-7的零点所在的区间为（ ）
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
若函数f（x）=
（a＞0，且a≠1）在（0，+∞）上是增函数，则a的范围是（ ）
|
A、（0，
| ||
| B、（0，1） | ||
C、（0，
| ||
D、[
|