题目内容
16.若$({x+y})({\frac{1}{x}+\frac{a}{y}})≥16$对任意x,y∈R*恒成立,则正实数a的最小值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 9 |
分析 不等式(x+y)($\frac{1}{x}$+$\frac{a}{y}$)≥16对任意正实数x、y恒成立,可知:16≤[(x+y)($\frac{1}{x}$+$\frac{a}{y}$)]min.令f(x)=(x+y)($\frac{1}{x}$+$\frac{a}{y}$),(a>0).利用基本不等式即可得出其最小值.
解答 解:∵不等式(x+y)($\frac{1}{x}$+$\frac{a}{y}$)≥16对任意正实数x、y恒成立,
∴16≤[(x+y)($\frac{1}{x}$+$\frac{a}{y}$)]min.
令f(x)=(x+y)($\frac{1}{x}$+$\frac{a}{y}$)(a>0).
则f(x)=a+1+$\frac{ax}{y}$+$\frac{y}{x}$≥a+1+2 $\sqrt{\frac{ax}{y}•\frac{y}{x}}$=a+1+2$\sqrt{a}$.当且仅当y=$\sqrt{a}$x取等号.
∴a+1+2$\sqrt{a}$≥16,解得a≥9.
因此正实数a的最小值为9.
故选:D.
点评 本题考查了恒成立问题的等价转化、基本不等式的应用,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
7.设m、n是两条不同的直线,α、β是两个不同的平面,则( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m∥n,n⊥α,则m⊥α | C. | 若m∥α,m∥β,则α∥β | D. | 若m∥α,α⊥β,则m⊥β |
1.对任意a∈R,曲线y=ex(x2+ax+1-2a)在点P(0,1-2a)处的切线l与圆C:(x-1)2+y2=16的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 以上均有可能 |
5.函数$f(x)={(6-x-{x^2})^{\frac{3}{2}}}$的单调递减区间为( )
| A. | $[{-\frac{1}{2},2}]$ | B. | $[{-3,-\frac{1}{2}}]$ | C. | $[-\frac{1}{2},+∞)$ | D. | $(-∞,-\frac{1}{2}]$ |
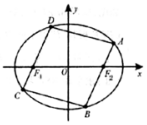 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴的一个顶点与两个焦点构成正三角形,且该三角形的周长为6
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴的一个顶点与两个焦点构成正三角形,且该三角形的周长为6