题目内容
用反证法证明命题“自然数a，b，c中三个均为偶数”的反设（ ）
| A、全是奇数 |
| B、恰有一个偶数 |
| C、至少有一个偶数 |
| D、至多有两个偶数 |
考点：反证法与放缩法
专题：证明题,反证法
分析：用反证法法证明数学命题时，假设命题的反面成立，写出要证的命题的否定形式，即为所求．
解答：
解：用反证法法证明数学命题时，应先假设要证的命题的反面成立，即要证的命题的否定成立，
而命题：“自然数a，b，c中三个均为偶数”的否定为：“至多有两个偶数”，
故选：D．
而命题：“自然数a，b，c中三个均为偶数”的否定为：“至多有两个偶数”，
故选：D．
点评：本题主要考查用反证法法证明数学命题，求一个命题的否定，注意否定词语的应用，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f（x）=cosx，则f′（
）等于（ ）
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
已知直线a，b，c和平面α，β，γ，下列说法正确的是（ ）
| A、若a⊥b，b⊥c则a⊥c |
| B、若α⊥β，β⊥γ，则α⊥γ |
| C、若a∥α，b∥β，a∥b，则α∥β |
| D、若α∥β，β∥γ，则α∥γ |
若l，m，n是互不相同的空间直线，α，β是不重合的平面，下列命题正确的是（ ）
| A、若α∥β，l?α，n?β，则l∥n |
| B、若α⊥β，l?α，则l⊥β |
| C、若l⊥n，m⊥n，则l∥m |
| D、若l⊥α，l∥β，则α⊥β |
经过点M（2，2）且在两轴上截距相等的直线是（ ）
| A、x+y=4 |
| B、x+y=2 |
| C、x=2或y=2 |
| D、x+y=4或x=y |
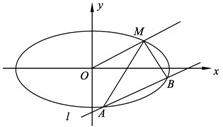如图所示，已知椭圆的中心在原点，焦点在x轴上，长轴长是短轴长的3倍且经过点M（3，1）平行于OM的直线l在y轴上的截距为m（m≠0），且交椭圆于A，B两不同点．