题目内容
已知函数f（x）=x3-x2+1，则f（x）在点（1，1）处的切线的倾斜角为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：利用导数研究曲线上某点切线方程,直线的倾斜角
专题：导数的综合应用
分析：求出函数的导数，利用导数的几何意义即可得到切线斜率，从而得到切线的倾斜角．
解答：
解：∵函数f（x）=x3-x2+1，
∴f′（x）=3x2-2x，
则f′（1）=3-2=1，
即在点（1，1）的切线的斜率k=1，
由tanθ=1，解得θ=
，
则对应的切线的倾斜角为
，
故选：B
∴f′（x）=3x2-2x，
则f′（1）=3-2=1，
即在点（1，1）的切线的斜率k=1，
由tanθ=1，解得θ=
| π |
| 4 |
则对应的切线的倾斜角为
| π |
| 4 |
故选：B
点评：本题主要考查函数切线的倾斜角的计算，利用导数的几何意义求出切线斜率是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
直线l1与直线l2：3x+2y-12=0的交点在x轴上，并且l1⊥l2，则l1在y轴上的截距是（ ）
| A、-4 | ||
| B、4 | ||
C、-
| ||
D、
|
已知函数f（x）=cosx，则f′（
）等于（ ）
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
下列给变量赋值的语句正确的是（ ）
| A、3=a |
| B、a+1=a |
| C、a=2*b-1 |
| D、a=b=c=3 |
已知点A（2，-1，-3），则点A关于x轴的对称点A的坐标为（ ）
| A、（2，1，-3） |
| B、（-2，-1，-3） |
| C、（-2，1，3） |
| D、（2，1，3） |
已知点Q（0，2
）及抛物线y2=4x上一动点P（x，y），则x+|PQ|的最小值是（ ）
| 2 |
| A、2 | ||
| B、3 | ||
C、
| ||
D、2
|
已知直线a，b，c和平面α，β，γ，下列说法正确的是（ ）
| A、若a⊥b，b⊥c则a⊥c |
| B、若α⊥β，β⊥γ，则α⊥γ |
| C、若a∥α，b∥β，a∥b，则α∥β |
| D、若α∥β，β∥γ，则α∥γ |
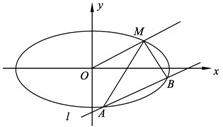如图所示，已知椭圆的中心在原点，焦点在x轴上，长轴长是短轴长的3倍且经过点M（3，1）平行于OM的直线l在y轴上的截距为m（m≠0），且交椭圆于A，B两不同点．